本文是我对01背包问题的理解,在本文中具体分析dp数组的形成过程,最核心的地方就是我对每种情况下的01背包问题给出了代码运行结果,便于读者理解。
重点解释了为什么一维dp数组的01背包问题为什么要倒叙遍历背包,以及为什么不能先遍历背包,只能先遍历物品。
1,一维dp数组为什么不能正序遍历书包?
因为正序遍历背包会导致同一个物品被放了两次,但是01背包要求同一物品只能被放一次。
2,一维dp数组为什么不能先遍历背包?
因为能用一维dp数组解决01背包问题的原理就是先遍历物品时dp数组是一行一行形成的(),下一行的数据只受到上一行数据的影响,因此可以只用一维数组去解决01背包问题,但是先遍历书包时dp数组时一列一列形成的(),这二者本质上就是相悖的,如果要强行理解的话,就是如果先遍历背包时,只会往背包中放入一件物品()。
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大
举例说明:假设背包最大重量为4,物品的重量以及价值如表所示:
下面分别通过二维db数组以及一维dp数组进行分析。
dp[i][j]:从物品0到物品i中任意取,放入容量为j的背包,可放入物品的最大价值为dp[i][j]。
递推关系式的含义为:01背包问题可以分解为不放物品i和放物品i
即dp[i][j]为放物品i和不放物品i的得到的价值的最大值。
2.1先遍历物品
根据代码随想录的介绍,二维dp数组的01背包问题先遍历物品还是先遍历背包均可。
如果先遍历物品,代码如下:
其中为了看到每次遍历后dp数组的变化,我将其打印输出,以便分析。
代码运行结果如下:
dp数组形成过程

先遍历物品时,整个dp矩阵的下一行数据由上一行数据计算得到,。
2.2.先遍历背包
同理先遍历背包再遍历物品可以得到相同结果,但是此时由于遍历顺序的改变,dp数组的形成过程发生了变化,首先附上代码:
代码运行结果如下:
dp数组形成过程
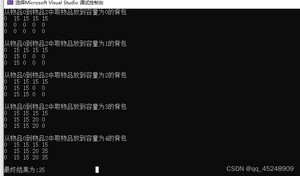
由不同的遍历顺序的运行结果可知,先便利物品时dp数组是一行一行形成的,而先遍历背包时,dp数组是一列一列形成的。
如果先遍历物品,则其思想为从物品0到物品i中选物品放入容量为4的背包中得到的最大价值,其中i由0取到2。
如果先遍历背包,则其思想为从物品0到物品2中选物品放到容量为j的背包中得到的最大价值,其中j由0取到4。
根据递推关系式可知 dp[i][j] 与 i-1 行的 0 到 j-1 这些数据有关,这个思想对理解一维dp数组为什么倒序遍历很有用。
二维dp数组的01背包问题较好理解,下面介绍一维dp数组的01背包问题。
利用滚动数组的形式将二维数组降为一维数组,目前考虑先遍历物品的情况,后续分析先遍历背包的情况。
可以写成一维形式的原因在上述二维dp数组中其实已经略微阐述了一下,现在进行详细分析。
在上述分析中,我们知道dp[i][j] 只与 i-1 行的 0 到 j-1 这些数据有关,即dp矩阵的下一行数据只与上一行的一些数据有关,因此完全可以利用一维数组重复使用。
此时dp[j]的含义为:容量为j的背包可以背的最大价值。
背包倒序遍历
下面分析一下先遍历物品时的一维dp数组解决01背包问题的代码,注意此时是倒序遍历背包:
运行结果为:

可以看到dp数组的形成过程与二维dp数组的形成过程一致,只不过此时的dp数组是一维的,把三个一维dp数组拼在一起便形成了二维dp数组的形式。
背包正序遍历
在一维dp数组求解01背包问题中很重要的一点就是书包的遍历顺序,此时书包的遍历顺序只能是倒序遍历,具体原因如下:
首先先将代码改成正序遍历的形式,具体代码在此不再赘述,只需要把上述代码的循环改成如下形式:
代码运行结果如下:
可以发现结果不一样了,我们只看第一组数据来分析一下产生这种现象的原因,即从物品0中取物品放到背包中得到的结果为
对比二者可以很容易发现以下现象:
从递推关系式出发:
可以发现正序遍历时计算 dp[2] 时把 dp[1]=15 加上去了,意味着物品0被放入了两次,但实际上加的应该是dp[1]=0 。换种方式理解就是dp[2]的正确计算方式应该是上一行的dp[1]加上15,而如果正序遍历的话,便使得dp[1]的值发生了改变,此时计算的是本行的dp[1]加上15。
因此需要倒序遍历使得每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
上述代码及分析均基于先遍历物品,现在分析先遍历背包时的情况。首先从上述分析中我们可以知道,先遍历背包时,二维dp数组是一列一列形成的,但是此时我们用一维dp数组时,我们只能按行形成dp数组,所以只能先遍历物品。
如果非要先遍历背包,可以将上述代码中的循环代码写成如下形式:
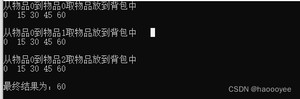
运行结果如下:

首先结果是错误的,这是由于先遍历背包时我们每次只往背包中放入一件物品,所以在背包容量为4时的结果为:
1,一维dp数组为什么不能正序遍历书包?
因为正序遍历背包会导致同一个物品被放了两次,但是01背包要求同一物品只能被放一次。
2,一维dp数组为什么不能先遍历背包?
因为能用一维dp数组解决01背包问题的原理就是先遍历物品时dp数组是一行一行形成的(),下一行的数据只受到上一行数据的影响,因此可以只用一维数组去解决01背包问题,但是先遍历书包时dp数组时一列一列形成的(),这二者本质上就是相悖的,如果要强行理解的话,就是如果先遍历背包时,只会往背包中放入一件物品()。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/10247.html

