背景
随着互联网行业的井喷式发展,获取信息的方式越来越多,人们从主动获取信息逐渐变成了被动接受信息,信息量也在以几何倍数式爆发增长。举一个例子,PC时代用google reader,常常有上千条未读博客更新;如今的微信公众号,也有大量的红点未阅读。垃圾信息越来越多,导致用户获取有价值信息的成本大大增加。为了解决这个问题,我个人就采取了比较极端的做法:直接忽略所有推送消息的入口。但在很多时候,有效信息的获取速度极其重要。
由于信息的爆炸式增长,对信息获取的有效性,针对性的需求也就自然出现了。推荐系统应运而生。
推荐形式
电商网站常见的推荐形式包括三种:
- 针对用户的浏览、搜索等行为所做的相关推荐;
- 根据购物车或物品收藏所做的相似物品推荐;
- 根据历史会员购买行为记录,利用推荐机制做EDM或会员营销。
前面2种表现形式是大家可以在网站上看到,而第3种表现形式只有体验后才能知晓,一封邮件,一条短信,一条站内消息都是它的表现方式。
下面将对亚马逊中国的前两种表现形式进行简单说明:
● 对于非登录用户,亚马逊中国在网站首页和类目栏,会根据各个类目畅销品的情况做响应的推荐,其主要表现形式为排行榜。搜索浏览页面以及具体的产品页面的推荐形式则有关联推荐(“经常一起购买的商品”)和基于人群偏好的相似性推荐(“购买此物品的顾客也购买了”、“看过此商品的顾客购买的其他商品”)。
● 对于登录用户,亚马逊中国则给出了完全不同的推荐方式,网站会根据用户的历史浏览记录在登入界面首屏展现出一个今日推荐的栏目,紧接着是最近一次浏览商品的记录和根据该物品所给的产品推荐(“根据浏览推荐给我的商品”、“浏览XX产品的用户会买XX的概率”),值得注意的是,每个页面最下方网站都会根据用户的浏览行为做响应推荐,如果没有浏览记录则会推荐“系统畅销品”(13页,50款商品)。
推荐系统常见的架构体系如下:
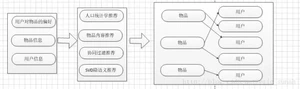
从架构图可以看出,一个简单的推荐系统通常包括三个部分
1. 数据来源
该部分至少包括三部分内容:
● 物品信息
● 用户信息,例如用户爱好,浏览记录,购买记录等
● 用户的物品的偏好,例如 商品评分,商品评论等
2. 算法处理:常见的算法类型主要包括
● 人口统计学推荐:主要是根据用户资料信息,发现和物品的相关程度
● 物品内容推荐:根据用户的偏好,推荐相似的物品给用户
● 协同过滤推荐:根据用户对物品的偏好,发现物品或是用户的相关性,然后基于相关性进行推荐,主要包括:1:基于用户的推荐 2:基于物品的推荐
● SVD(奇异值分解):相当于协同过滤的相似度计算模型,主要基于用户和物品信息构成的矩阵,矩阵中的值是用户对商品的评分,这个矩阵通常是一个比较稀疏的矩阵,通过SVD算法可以得到用户与物品的特征向量PU(用户的偏好),PI(物品的偏好)通过PU*PI得到用户对物品的评分预测
3. 结果展示:对推荐结果进行展示
本章节主要介绍 协同过滤,SVD, K-Means 三种算法
协同过滤模型
模型介绍
协同过滤Collaborative Filtering (CF)算法是推荐算法的一个大分支,基本思想是推荐相似的物品,或者推荐相似用户(隐式或者显式)评分过的物品。CF方法主要可以分为两类:基于邻域和基于隐语义。
1. 基于邻域的方法利用“两个用户共同评分过的物品”(user-based)或者“共同评价两个物品的用户”(item-based)分别计算用户间的相似度和物品间的相似度。而相似度的计算有余弦相似度,皮尔逊相似度和一种被称为“Conditional Probability-Based“的Similarity。皮尔逊系数与余弦相似度的不同在于,皮尔逊系数还能捕捉负关系,第三个方法的弊端在于由于每个物品(人)邻域的大小不同,流行物品或评分多的用户会引起问题。因此,实际中一般采用带权的皮尔逊相似度(P. 2) 。但基于邻域方法的缺点是:由于实际用户评分的数据是十分稀疏,用户之间可能根本没有相同的评论;而且用启发式的方法很难考虑全面用户和物品之间的所有关系。
2. 基于隐语义的方法则不依赖于共同评分。其基本思想是将用户和物品分别映射到某种真实含义未知的feature向量。用户feature代表用户对不同类别电影的喜好程度(如:动作片5,惊悚片5),物品feature代表电影中大致属于哪类电影(如:爱情片3,喜剧片5)。然后通过两个feature向量的内积来判断用户对一个物品的喜好程度。虽然这个方法不要求共同评分,但推荐系统还是面临很大的数据稀疏问题。
算法逻辑
作为CF的两大基本分类,邻域的相关算法比较简单不再介绍,本文主要介绍SVD,不过在介绍SVD之前,先对K-Means做个简单的说明
K-means
算法介绍
推荐系统大多数都是基于海量的数据进行处理和计算,要在海量数据的基础上进行协同过滤的相关处理,运行效率会很低,为了解决这个问题通常是先使用K-means对数据进行聚类操作,说白了,就是按照数据的属性通过K-Means算法把数据先分成几大类,然后再在每个大类中通过邻域或是隐语义算法进行推荐
算法逻辑
网上有很多关于K-Means算法的描述,个人觉得大多数都很拗口,不容易理解,下面这个图中举例的方式,感觉比较容易理解
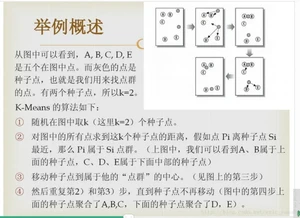
在Python的sklearn库中已经实现了该算法,如果有兴趣也可以实现一个自己的K-Means算法。
K-Means算法在实际运行的过程中存在以下几个问题
1. 最大问题是:K值对最后的结果影响较大,但是该值是由用户确定的,且不同的数据集,该值没有可借鉴性
2. 对离群数据点敏感,就算少量的离群数据也能对结果造成较大的影响
3. 算法初始化中心点的选择好坏,会直接影响到最终程序的效率
为了解决上面的问题,出现了二分KMeans算法,有兴趣的读者,可以自行寻找相关的资料 ,本文不做详细介绍
SVD
算法介绍
特征值分解是一个提取矩阵特征很不错的方法,但是它只是对方阵而言的,在现实的世界中,我们看到的大部分矩阵都不是方阵,比如说有N个学生,每个学生有M科成绩,这样形成的一个N*M的矩阵就不可能是方阵,我们怎样才能描述这样普通的矩阵呢的重要特征呢?奇异值分解可以用来干这个事情,奇异值分解是一个能适用于任意的矩阵的一种分解的方法。
算法逻辑
算法公式:
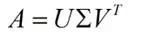
公式说明:假设A是一个N * M的矩阵,那么得到的U是一个N * N的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),Σ是一个N * M的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),V’(V的转置)是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量),从图片来反映几个相乘的矩阵的大小可得下面的图片
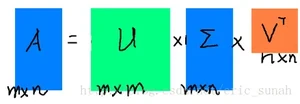
那么奇异值和特征值是怎么对应起来的呢?首先,我们将一个矩阵A的转置 *A,将会得到一个方阵,我们用这个方阵求特征值可以得到:
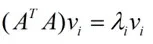
这里得到的v,就是我们上面的右奇异向量。此外我们还可以得到:
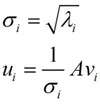
这里的σ就是上面说的奇异值,u就是上面说的左奇异向量。奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解
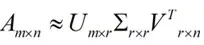
r是一个远小于m、n的数,这样矩阵的乘法看起来像是下面的样子
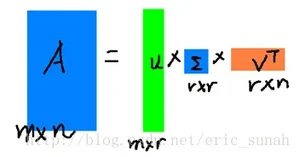
边的三个矩阵相乘的结果将会是一个接近于A的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积 越小,存储量就越小)要远远小于原始的矩阵A,我们如果想要压缩空间来表示原矩阵A,我们存下这里的三个矩阵:U、Σ、V就好了。
在Numpy的linalg中,已经对SVD进行了实现,可直接进行使用
公共函数
该部分主要是用来加载样本数据的代码
使用邻域法进行推荐
使用SVD进行推荐
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/10978.html
