这也许是你全网你能找到的最详细的倒排索引的底层解读。博主把倒排索引的讲解划分为以下七个部分，理解难度递增，可根据自身需要选择依次阅读或者针对性阅读。
通常来说，应付一般的面试，理解第一部分即可。如果需要面试搜索相关业务的岗位，需要深层次理解倒排索引，可根据自身情况选择阅读。
本文花费了作者大量的精力来论证和整理，如果你喜欢作者的文章，请帮忙点个赞和关注吧 O(∩_∩)O ~。谢谢大家的支持。
提到ES，大多数爱好者想到的都是搜索引擎，尽管这是个误区，但是也不得不提。大数据搜索最重要的三个要素分别是 “快”、“准”、“高”。
所谓快，即搜索速度要快，搜索引擎级别的要求要达到PB级数据的秒内搜索；
所谓“准”，即搜索结果要尽量符合正常人类的预期值，在ES里我们用这个概念来描述搜索结果的准确性。ES里计算相关性采用“打分机制”，ES在旧版本中使用一种叫TF/IDF的评分算法作为默认的评分算法，从 7.x 之后，默认改为BM25评分算法。
关于 BM25 算法的原理解读，推荐阅读我的博客：Elasticsearch相关度评分算法（三）：BM25（Okapi BM25）
天下武功，唯快不破。本节内容，我将围绕“ES是如何支撑大数据近实时搜索”这一话题展开，这一点非常重要。聪明的人类在探索快速检索这一技术领域已经发挥了令人难以想象的智慧，后人不必重复造轮子，要学会如何站在巨人的肩膀上。这一点，前人已经帮助我们总结很多经验。概括的说，一个优秀的搜索引擎的设计，至少应该具备以下几点要求：
- 高效的压缩算法
- 快速的编码和解码算法
- 合理的数据结构
- 通用最小化算法
结合以上几点，后面我将通过一个案例来讲解，倒排索引的基本原理是什么。在了解“倒排索引”之前，我们先来看一下何为“索引”。
一本汉语字典，如果我们想要从中找到某个字，通常我们会通过字典最前面的拼音检索或者是部首检索来查找。其实汉语字典的正文本身就是一个索引，比如我们要查找“吴”字，很自然的就想到了“吴”的拼音是“wu”，w在26个字母中在很靠后的位置，基本上就可以确定“吴”字的大致位置，然后按照字典序可以在w字母的汉字里精确的找到这个字，因为汉字本身就是按照字典序排列的，这种按照一定规则排序的目录在关系型数据库中一般叫做“聚集索引”。
除了这种索引，通常我们还了解一种类似于“偏旁部首”的检索方式称之为“非聚集索引”，我们这里不展开来讨论什么是聚集索引和非聚集索引。但是我们可以确定的是，不管是什么索引，它的目的都是帮助我们快速检索数据的。
在数据库领域里，索引可以概括为一种帮助我们快速检索数据的以文件形式落地的数据结构。
以MySQL为例，如图1-1所示：
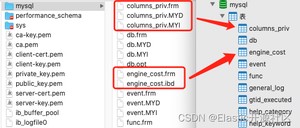
左侧是MySql安装文件的data目录，右侧使我们使用数据库客户端打开数据库后的样式，左侧文件分别对应了右侧数据库中的数据库名，我们以“mysql”这个数据库为例，文件夹中每个文件都有若干个不同后缀的同名文件，分别对应右侧某个数据表，不同的后缀代表不同的数据类型，其中.frm文件代表当前文件存储的是数据表的表结构，.MYD和.MYI文件则代表了当前文件是myisam存储引擎下的数据文件和索引文件，.ibd则代表当前文件是innodb存储引擎下的索引文件，只不过innodb的数据和索引使用了同一个文件。
不管是元数据还是索引数据，他们最终都是以“文件”的形式存储在磁盘中的，只不过不同的文件内部使用的数据结构各不相同。而MySql使用的数据结构是B+Trees。但是这种数据结构并不适用于倒排索引，原因我们会在后面的文章中提到。
理解了索引的定义，我们来看一下索引在生活场景中的实际应用。如图1-2所示：
我们假设右侧表格是某个商城软件的商品表，当我们有通过关键字搜索商品列表的需求的时候，我们会执行图中左侧的SQL语句进行模糊查询，但是当数据量达到一定量的时候，搜索速度会很慢，原因是当前语句会造成“扫表”，产生大量的IO，MySql每次IO的大小默认为16KB，所以这样的查询是不被允许的，通常情况下解决的办法是在product字段上创建索引，但是这样做会产生很多问题。
首先，MySql使用的B+Trees的数据结构来存储索引数据，这种数据结构当数据量达到千万级的时候，那么每个单个节点会树的深度就已经达到甚至超过4层了，当数据量再大，查询的性能就达不到要求了，况且搜索引擎级别的数据量级动辄亿级或者十亿级，如果按照搜索引擎的要求，那这种数据结构是难以支撑的。
其次，因为每个树的每个节点大小固定为16KB，一般来说每个索引的占用的空间越大，那么单个节点所容纳的索引数量就越少。虽然B+Trees的非叶子节点不存放data，只存放索引数据，但是由于关键字搜索的需求就是在文本字段上去创建索引，所以通常我们的索引Key也都是文本类型，这就造成了单个索引占用的空间较大，B+Trees非叶子节点不存放数据这种设计相较于B-Trees（B Trees）本身就是为了减轻非叶子节点的负重，从而降低树的深度，但是显然我们这样做就违背了这一B+Trees的设计初衷，显然在文本上创建索引并不是很明智的选择，当索引字段为长文本的时候，树的深度会成指数级加大。
而且通常情况下我们有模糊查询的需求，需要在搜索的时候前后加上“%”，但由于“最左匹配原则”，左like查询会导致索引的失效，导致SQL查询性能指数级下降。况且即便索引不会失效，目标字段的关键词中往往掺杂着一些无用字符，比如我们要查找的商品叫做“小米NFC旗舰手机”，但是我们搜索的关键词是“小米NFC手机”或者“小米手机NFC”，这种由于词序颠倒或者有干扰字符的情况就会导致我们的搜索结构不准确。
综上所述，B+Trees支撑的索引并不适合做“关键词搜索”这种需求。
那么，Lucene中的倒排索引是如何解决这类问题呢？同样我们以上文提到的场景为例，如图1-3所示：
Lucene首先会把目标域（field）的所有行进行分词操作，就是把product字段对应的短语切分成若干个词项（Term），这里其实英文有天然的优势，因为每个词项都是以空格切分的，如果是中文就要用到中文分词器，不同的分词策略的分词结果大相径庭。关于分词器，笔者会在后面内容中详细介绍。这里我们按照正常人类的思维暂且以图中空格作为切分依据，如“新款小米至尊纪念版手机”我们暂且认为分词后包含了“新款”、“小米”、“至尊”、“纪念版”、“手机”这么几个词项，以此类推，Lucene会在Index time把索引字段的所有词项切分计算出来，并且按照字典序生成一个词项字典（Term Dictionary），此项字段存储的是去重之后的所有词项。我们假设上图左侧的表格中term dictionary字段就是最终生成的词项字典，那么右侧的倒排表（Posting List）保存的就是所有包含当前词项的元数据的id的有序int数组。当然实际存储的这两种数据结构真正的情况远比我们目前看到的复杂的多，但是它们实际的样子并不便于我们理解什么是倒排索引，因此我们暂且以这种“二维表格”的形式来展示这两种数据结构。至于Term Index，我们暂时不必理会，只需要知道，这张表格里包含的三种数据结构便组成了我们经常提到的“倒排索引”。
当我们按照上述所说进行一定的分词策略创建倒排索引之后，假如最终的结果就如上面图中所示。此时加入用户搜索的关键词为“小米NFC手机”，按照相同的分词策略，用户的搜索词会被分成“小米”、“NFC”、“手机”三个词项，我们分别对三个词项在左侧表格也就是我们暂时理解的“倒排索引”文件中进行检索。此时的查询由原本的模糊查询编程了精准查询，比如“小米”这个关键词，匹配到了就是匹配到了，如果匹配到了也没必要继续检索下去了，因为后面不可能再有相同的词项了。这种查询会大大加快查询的速度，比如“小米”这个关键词，最好的情况可能只匹配了第一次就命中了索引，假如元数据有10亿条，并且在这10亿数据中可能包含“小米”这个关键词的数据超过了100W行，那么本次查询只检索了一次就找到了元数据中包含“小米”这个关键词的一百万+条数据，不可谓不高效！当然了，检索也不可能次次都是一次命中，不过ES底层对倒排索引的检索做了大量的优化，大大提高了倒排索引的检索效率，比如Term Index就是词项字典索引，可以大大加快倒排索引的查询效率，关于词项索引（词项索引）我会在后面的内容中详细介绍，此处不再赘述。
回过头来继续看当前的案例，假设每个词项在倒排索引中命中之后，我们都做一个“命中”标记，那么当前搜索的三个词项都命中了对应的Term，我们计算一下此次命中的倒排表中的id分别命中了多少次。假如此次搜索倒排表中包含了元数据中id为1，2，3，4这几条数据，我们分别计算一下每个id被命中的次数，并且把对应的结果抽象出一个字段放在元数据表格的右侧，那么这个结果就可以暂时理解为一个简单的“相关度”。我们按照这个“相关度”倒序排列元数据，就会发现，当前这个顺序基本就是符合我们正常人类对搜索结果的一个预期排序。最符合预期的结果会被排在最上面，最不符合的结果排在最下面。
到此为止，上图左侧的表格就可以看成是“倒排索引”，那么整个这个检索的过程就叫做“全文检索”。
索引文件中分别存储了不同的数据
其中倒排表包含某个词项的所有id的数据存储了在.doc文件中；
词项字典包含了index field的所有经过normalization token filters处理之后的词项数据，最终存储在.tim文件中。
所谓normalization其实是一个如去重、时态统一、大小写统一、近义词处理等类似的相关操作；词项索引就是为了加速词项字典检索的一种数据结构，落地文件为.tip。.tip文件和.tim文件的数据结构如下图2-2所示：
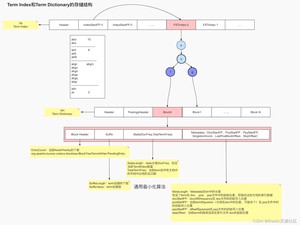
Lucene中通过FST Index信息来读取当前域在索引文件.tim的具体信息，而同一个索引所有域的FSTIndex都被连续的写入在同一个.tip文件中，所以就需要indexStartFP 来索引 FSTIndex。
FSTIndex底层是一个字节数组，存储了每个Block在.tim中的起始位置，如上图2-2所示，Block f 和Block g 对应的 Block 分别被保存在了.tim文件的 Block 0 和 Block 1 的位置。
每个Block内部又保存了Block Header、Suffix和Stats信息以及Metadatas信息，其中Block Header中存储了当前Block中的Pending Block和Pending Term的总计数，也就是EntryCount，Sufix则是保存了当前Block后缀的个数以及分别是什么，如block b的SufixLength=2，为f、g。Stats则保存了当前Term的词频和文档频率，参见：org.apache.lucene.index.TermsEnum.TermStats。
其中docFreq为包含当前Term的doc数量，totalTermFreq为当前term在所有文档中的当前字段中出现的总次数，但实际保存的是和docFreq的差值，这也是遵循通用最小化算法的法则表现。需要注意的是，两者均是指在同一个域内的计数。Metadatas这里不着重介绍。
关于倒排表的文件结构，我们仅需知道其内部存储了包含Term的id数组、词频、postion、payload、offset等信息，需要重点注意的是ES内部采用怎样的压缩算法。这一点在下一节内容展开来讲。
既然全文检索经常被用在“大数据检索”这一应用领域，搜索引擎级别的数据量级通常通常在亿级甚至十亿级上，那么也就说如果我们对其建立倒排索引，每个字段被拆分成了若干Term，结果就有可能导致倒排索引的数据量甚至超过了source data，即便我们对倒排索引的检索不必全表扫描，但是太多的数据不管是存储成本还是查询性能可能都不是我们想要的，解决办法就是采用高效的压缩算法和快速的编码和解码算法。
以第一节中的场景为例，假设我们的商品有10亿个，某个Term如“小米”，包含当前词项的docs假如有100万条，每个docid为int类型，占用4个Bytes，也就是32个bit，换算成MB，就是400万字节总占用大小为3200万个bit≈3.8MB。粗略的看，也许你并不觉得3.8MB有多大，但是需要注意的是，倒排索引的数量级很有可能也是亿级甚至更多，这样算来，数据的压缩就是我们不得不考虑的事情。
我们还是以“小米”这个Term为例，加入其对应的倒排表中的id为“[1,2,3…100W]”，我这里有字母W代表万。通常一个数值类型占用的bit数取决于其值的大小，这是数值存储的计算方式决定的，一个bit所能存储的数字个数是21，能存储的最大值就是21-1，也就是[0,1]，同理2个bit的取值范围就是[0,22）或[0,22-1]，其计算公式为n个bit能存储数值的区间为[0,2n)，比如int使用32个bit存储，最大值就是231-1，这里之所以是31次方是因为int是有符号整型，其中一个bit用来存储符号位了，但是由于docId只有正整型，因此在倒排索引的常经理不必考虑负数的情况。那么当前数组中最大值只有100W，我们就可以使用更少的bit来存储，而不是32个bit，那么具体用多少个呢，原则上是2n只要大于100W，n取最小值就可以了，此时n=20。但此时数组中每个数值都需要使用20个bit来存储，这显然是极大的浪费，因为数组前段的数值都非常小，仅用很少的bit就可以存储，这时我们就考虑是否可以用差值存储（dealta list），即不存储原本的数值，而是存储每个数值与前一个数字的差值，这时原本的数字组就变成了[1,1,1…1]，数组中共包含100W个1，如果存储数字1，那么用1个bit就足够存储，也就是我们存储一百万个数字，只需要用100万个bit，虽然看上去还是很多，但是原本存储这些数据需要使用3200W个bit，现在数据压缩了32倍，这也是采用差值存储的理论最该的压缩倍率。如图3-1：
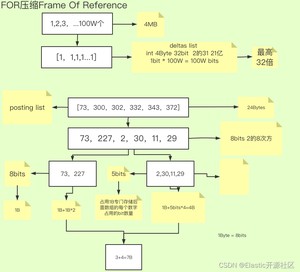此时或许你已经有了疑惑，实际场景中不可能有这么巧合的情况。没错，那我们以图3-1中的数组[73，300，302，332，343，372]为例，此数组占用的空间大小为4Bytes*6=24Bytes，计算差值列表，结果为[73，227，2，30，11，29]，取差值的目的就是压缩整个数组的取值范围。经过计算后，最大值为227，使用8个bit来存储。但是细心思考可以发现，除了227意外，其他数字都很小，如果都是用8个bit来存储，那么显然浪费了不少存储空间。于是我们尝试将数组进行拆分，将原本一个数组拆分成[73，227]和[2,30,11,29]两个数组，这样做的好处就是第二个数组的数值区间进一步减小了，最大值由227变为了30，这时只需要5个bit就可以存储任意一个数字。而第一个数组还是使用8个bit存储每一个数字。然而问题又来了，为什么我们不对每一个数字单独使用其最合适的bit数来存储，这样岂不是更节省空间么？这就要再次提到关于数据存储的法则“快速的编码和解码”，我们不仅需要把数据尽可能的压缩使其占用更小的空间，还需要对齐进行解码，因为我们最终需要的还是source data，我们deltas list进行拆分的目的是对每个数组使用不同的bit进行合理的空间分配，在这个过程中我们需要对每个数组数组元素使用的bit数进行记录，比如[73，227]这个数组每个数字使用8个bit来存储，这个数字“8”是需要一段空间来记录的，笔者暂且把这块记录空间叫Record Space，这块空间的大小是1个Byte。如果我们把每个数字单独拆分出来，那么也就是我们需要对每个数字单独再开辟出这个1个Byte的空间，得不偿失。所以在计算数组的拆分长度的时候就要权衡得失，尽量把数组保留的足够长，数组越长Record Space所占用的空间越可以忽略不计，但同时数组越扁平越好，取值区间越小越好。比如这个数组：[22, 43, 21, 34, 55, 64, 4322, 345]，就可以吧4322和345拆分出来，因为4322加大了每个数字的bit占用，造成了空间浪费。
最后我们来计算一下经过压缩后的磁盘占用。数组经过拆分，分为了两个数组，第一个数组每个数字占用1个Byte，共两个数字，总占用为2Bytes，记录数组单位大小的Record Space大小为1Byte，第二个数组每个数字占用5个bit，一共四个数字，共计20bit，但是计算空间的最小单位是Byte，所以实际占用的大小为3Bytes，第二个数组的Record Space大小也是1Byte，因此压缩后的数据总大小为1B+2x1B+3B+1B=7Bytes，相比压缩之前，大小不到原先的三分之一。
如果你足够细心，你也许会发现其实上述例子中的数组仍然具有一定的特殊性。没错，他是一个稠密数组，可以理解为是一个取值区间波动不大的数组。如果倒排表中出现这样的情况：[1000W, 2001W, 3003W, 5248W, 9548W, 10212W, … , 21Y]，情况将会特别糟糕，因为我们如果还按照FOR的压缩算法对这个数组进行压缩，我们对其计算dealta list，可以发现其每个项与前一个数字的差值仍然是一个很大的数值，也就意味着dealta list的每个元素仍然是需要很多bit来存储的。于是Lucene对于这种稀疏数组采用了另一种压缩算法：RBM（Roaring Bitmaps）
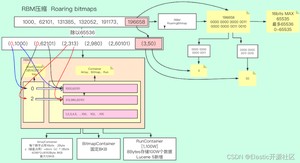
我们以图3-2中的数组 [1000，62101，，，，] 为例，这是一个典型的稀疏型数组。在进行数据压缩的时候，其实不管何种方法，我们的最终目的都是把原来的数字转换成足够小的数字以便于我们存储，同时又必须保证压缩后的数据是可以快速解码的。“减法”不好用，这次我们尝试使用“除法”。由于无符号int类型的最大值不超过232，因此RBM的策略就是把一个int型拆成两个short型的乘机，具体做法是把数组中的每个元素对216取模，因为被除数是232除数是216，因此商和余数均小于216。其实这种想法是国内开发者强行转化的逻辑，RBM算法本身的设计思路是将原数字的的32个bit分为了高16位和低16位。以原数组中的这个id为例，将其转化为二进制结果为 0，我们看到其实结果是不足32bits的，但因为每个int型都是有32个bit组成的，不足32bit会在其前面补0，实际其占用的空间大小仍然为32bits，如果这一点不理解，打个比方，公交车有32个座位，无论是否坐满，都是使用了32个座位。最终转换成二进制就是0000 0000 0000 0011 0000 0000 0011 0010，前16位就是高16位，转换成十进制就是3，后16位也就是低16位，转换成十进制就是50，3和50分别正好是除以63326（216）的得数和余数，换句话说，int类型的高16位和低16位分别就是其本身对216的商和模。
对数组中每个数字进行相同的操作，会得到以下结果：（0,1000）（0,62101）（2,313）（2,980）（2,60101）（3,50），其含义就是每个数字都由一个很大的数字变为了两个很小的数字，并且这两个数字都不超过65536，更重要的是，当前结果是非常适合压缩的，因为不难看出，出现了很多重复的数字，比如前两个数字的得数都是0，以及第2、3、4个数字的得数都是2。RBM使用了非常适合存储当前结果的数据结构。这种数据结构是一种类似于哈希的结构，只不过Key值是一个short有序不重复数组，用于保存每个商值，value是一个容器，保存了当前Key值对应的所有模，这些模式不重复的，因为同一个商值的余数是不会重复的。这里的容器官方称之为Container，如图3-3：RBM中包含三种Container，分别是ArrayContainer、BitmapContainer和RunContainer，下面我将对这三种Container展开来逐一讲解。
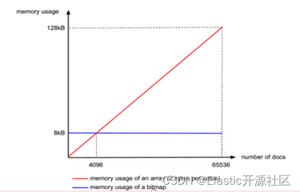
首先是ArrayContainer，顾名思义，Container中实际就是一个short类型的数组，其空间占用的曲线如图3-4中的红色线段，注意这里是线段，因为docs的数量最大不会超过65536，其函数为 y（空间占用）=x（docs 长度） x 2Bytes，当长度达到65536极限值的时候，其占用的大小就是16bit * 65536 / 8 /1024 = 128KB，乘以65536是总bit数，除以8是换算成Byte，除以1024是换算成KB。
第二种是BitmapContainer，理解BitmapContainer之前首先要了解什么是bitmap。以往最常见的数据存储方式都是二进制进位存储，比如我们使用8个bit存储数字，如果存十进制0，那二进制就是 0 0 0 0 0 0 0 0，如果存十进制1，那就是 0 0 0 0 0 0 0 1，如果存十进制2，那就是 0 0 0 0 0 0 1 1，用到了第二个bit。这种做法在当前场景下存储效率显然不高，如果我们现在不用bit来存储数据，而是用来作为“标记”，即标记当前bit位置商是否存储了数字，出的数字值就是bit的下标，如下图3-5所示，就表示存储了2、3、5、7四个数字，第一行数字的bit仅代表当前index位置上是否存储了数字，如果存储了就记作1，否则记为0，存储的数字值就是其index，并且存储这四个数字只使用了一个字节。
不过这种存储方式的问题就是，存储的数字不能包含重复数字，并且Bitmap的大小是固定的，不管是否存储了数值，不管存储了几个值，占用的空间都是恒定的，只和bit的长度有关系。但是我们刚才已经说过，同一个Container中的数字是不会重复的，因此这种数据类型正好适合用这种数据结构作为载体，而因为我们Container的最大容量是65536，因此Bitmap的长度固定为65536，也就是65536个bit，换算成千字节就是8KB，如图3-4中的蓝色线段所示，即Lucene的RBM中BitmapContainer固定占用8KB大小的空间，通过对比可以发现，当doc的数量小于4096的时候，使用ArrayContainer更加节省空间，当doc数量大于4096的时候，使用BitmapContainer更加节省空间。
第三种Container叫RunContainer，这种类型是Lucene 5之后新增的类型，主要应用在连续数字的存储商，比如倒排表中存储的数组为 [1,2,3…100W] 这样的连续数组，如果使用RunContainer，只需存储开头和结尾两个数字：1和100W，即占用8个字节。这种存储方式的优缺点都很明显，它严重收到数字连续性的影响，连续的数字越多，它存储的效率就越高。
一直以来，数据结构的“小”而“快”是每个追求更好性能的developer孜孜不倦追求的目标，所谓“快”即检索速度快，“小”即通用最小化算法。上一节我们介绍了倒排表的数据压缩原理和过程，自本节开始，我们分几部分详细介绍一下Lucene中对倒排索引Term DIctionary以及Term Index的数据压缩和优化算法。
我们已经了解到，Term Dictionary是字典序非重复的 K-V 结构的，而通常搜索引擎级别的倒排索引，Term Dictionary 动辄以“亿”起步，这势必要求我们在做数据存储时对其数据结构有极其高的要求。以图4-1为例，假设途中英汉词典片段就是我们要存储的词项字典，为了遵循“通用最小化算法”对其进行数据压缩，我们就必须要考虑如何以最小的代价换区最高的效率。通过观察不难发现，无论任何一个Term，无外乎由26个英文字母组成，这也就意味越多的词项就会造成的越多的数据“重复”。这里所说的重复指的是词项之间会有很多个公共部分，如“abandon”和“abandonment”就共享了公共前缀“abandonment”。我们是否可以像Java开发过程中对代码的封装那样，重复利用这一部分公共内容呢？答案是肯定的！Lucene在存储这种有重复字符的数据的时候，只会存储一次，也就是哪怕有一亿个以abandon为前缀的词项，“abandom”这个前缀也只会存储一次。这里就用到了一种我们经常用到的一种数据结构：Trie即字典树，也叫前缀树（Prefix Tree）。下面我们以Term Dictionary：（msb、msbtech、msn、wltech）为例，演示一下Trie是如何存储Term Dictionary的。
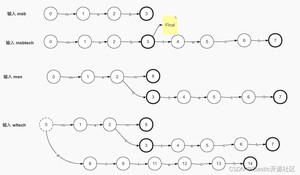
如上图4-2所示，我们按照每个Term一步来演示Trie是如何存储Term Dictionary的。图中我们以圆形标识节点，箭头代表节点的出度，出度存储了当前节点对应的字符。当输入词项“msb”的时候，如果图中第一步所示，图中以加粗的圆圈标识当前节点是一个终止节点。当输入第二个词项“msbtech”的时候，复用了“msb”，当输入“msn”的时候，节点2添加了第二个出度，至此我们已经实现了对重复关键字的复用。但是问题也就随之而来了，当最后一个Term输入的时候，节点0产生了第二个出度。
细心的你应该已经发现了，在使用字典树存储Term Dictionary的案例中，字符“tech”也属于重复部分，但是未被合理复用，导致了空间浪费。为了解决这个问题，Lucene采用了另一种数据结构：FST（Finite State Transducer），即“有限状态转换机”。FST是本章内容难点，也是倒排索引的核心数据结构。
通常我们在计算机的语言中标示一件事物，都会通过某种数学模型来描述。假如现在我们要描述一件事：张三一天的所有活动。这里我们采用了一种叫做FSM（Finite State Machine）的抽象模型，如图5-1所示，这种模型使用原型的节点标示某个“状态”，状态之间可以互相转换，但是转换过程是无向的。比如睡觉醒了可以去工作，工作累了可以去玩手机；或者工作中想去上厕所等等。在这个模型中，标示状态的节点是有限多个的，但状态的转换的情况是无限多的，同一时刻只能处于某一个状态，并且状态的转换是无序切循环的。
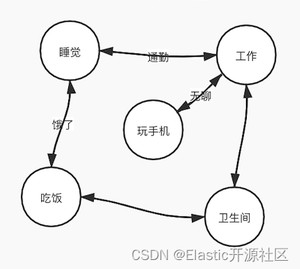
显然这种模型并不适用于描述Term Dictionary这样的数据结构，但是我们之所以提他，是为了方便读者理解这种具化事务抽象化描述的方式。虽然FSM并不适合，但是在他的基础上演化出了FSA（Finite State Acceptor）,我们仍然以图 4-2 中的Term Dictionary数据为例，演示一下FSA是如何在Trie的基础上进行优化的。
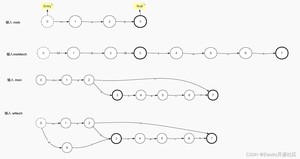
如上图5-2所示，相较于FSM，FSA增加了Entry和Final的概念，也就是由状态转换的不确定性变为了确定，由闭环变为了单向有序，这一点和Trie是类似的，但是不同的是，FSA的Final节点是唯一的，也是因为这个原因，FSA在录入和Trie相同的Term Dictionary数据的时候，从第三步开始才表现出了区别，即尾部复用。如果在第三步的时候还不太明显，那第四步中就可以清楚的看到FSA在后缀的处理上更加高效。
至此，FSA已经满足了对Term Dictionary数据高效存储的基本要求，但是仍然不满足的一个问题就是，FSA无法存储key-value的数据类型，所以FST在此基础上为每一个出度添加了一个output属性，用来表示每个term的value值。下面以Term Dictionary：（msb/10、msbtech/5、msn/2、wltech/8、wth/16）为例，演示一下FST的构建原理，斜线后面的数字代表每个term的输出值。
通用最小化算法的应用面非常广泛，这里其实也是遵循了这样的规则。可复用的不仅仅Term的字符，输出值之所以被存储了最靠前的位置上，目的也是为了让更多的Term复用，如果输出值产生了冲突，再去处理冲突问题，最终生成最小化FST。
如上图5-3所示，当第一个term:msb被写入FST中，其输出值被保存在了其第一个节点的出度上，在数据从FST中读取的时候， 计算其每个节点对应的出度的输出值以及终止节点的final output值的累加和，从而得出输出值，此时msb的输出值就是10+0+0+0=10，但是这里我用0来标识没有输出值，但实际情况没有输出值就是空而不是0，这里写0只是为了方便你去理解，这一点是需要注意的。
当第二个term:msbteach被写入的时候，其输出值5与msb的输出值10发生了冲突，这时，通用最小化算法法则再次发挥了功效。数字虽然不能像字符那样以前缀作为复用手段，但是数字是可以累加的，10可以拆成两个数字5，这样10和5就产生了公共部分，即5，所以这个时候m的输出值就需要改成5，那另一个5就需要找一个合适的位置，然而把它存放在任何一个节点的出度上似乎都会影响msbtech的计算结果，为了避免这个问题，可以把这个多出来的属于msb的输出值存入msb的final节点的final output中，节点的final output只会在当前出度是输入值的最后一个字符并且出度的target指向的是final节点的时候，才会参与计算。因此此时的msb和msbtech就各自把输出值存入了合适的位置，互不影响而且做到了“通用最小化”原则。
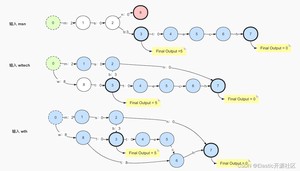
输入第三个term:msn，节点2产生了第二个出度：n，2 < 5，根据"通用最小化"法则，2和5有公共部分：2，5倍拆分成了2和3，此时公共前缀为“ms”，前面以“ms”为前缀的所有term都讲重新计算出度output，此时3需要满足：不能存放在公共前缀“ms”上，并且也不能在第二条出度“n”上，因此只能存放在出度b上，因为b在当前节点2第一条出度的链路上是最靠前的位置。这里FST和Trie最大的区别就是FST不仅使用了公共前缀，而且还计算了公共后缀，“msn”的最终节点会指向节点7，和节点6的出度h共享终止节点。
其实到这里还不能很好的提现“公共后缀”，但是输入wltech的时候，此时就产生了公共后缀“tech”，节点2的出度b和节点8的出度t共同指向了节点3。
输入最后一个term:wth，公共前缀为w，公共后缀为h，最终生成的FST如上图5-4所示。
FST的压缩率非常高，相比HashMap，FST的性能相差的并不多，但是可以大大的节省空间占用。“搜索引擎”级别的词项字典动辄几亿甚至几十亿的数量级，如果使用FST对其进行存储，其高效的数据存储使得数据被压缩的很小，使其完全缓存在内存中成为了可能。FST在Lucene中的应用非常广泛，比如同义词处理、模糊查询、Suggest等都有应用。
我之前提到过，在计算机编程语言的世界里，描述一件事情通常使用某种数据模型，如FSM。在Lucene中使用了一个了个泛型来描述FST的数据结构：org.apache.lucene.util.fst.FST，在FST对象的构建过程中，又使用了一个Node的类型的对象来描述FST模型中的“节点”，使用Arc来表示节点Node的出度。Lucene把Node分成了两种，分别是UnCompiledNode和CompiledNode，他们的区别就是是否“Compiled”，暂时可以理解为是否经过了某种处理，处理之后就是CompiledNode，否则就是UnCompiledNode，这里所说的“处理”指的就是构建FST对象中的一个过程。未处理过的Node也就是所有UnCompiledNode被放在了一个UnCompiledNode类型的数组中：UnCompiledNode[]
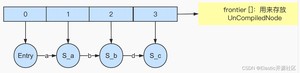
如图6-1所示，假设次数输入第一个Term，此时当前term所有的字符都不会被处理，因为FST的构建是遵循“尾部冻结”的规则的。那么什么是尾部冻结呢？首先我们知道FST最终会被构建成一个FST对象，那这个对象最终转换成二进制对象存储在一个BytesStore对象中，，在Lucene 8.7.0中，BytesStore中封装了一个byte[]类型的数组：current，current数组就是专门存储经过处理之后的节点（CompiledNode）的，当然经过处理后的节点以及其出度的信息都会被转换成二进制存储在current数组中，BytesStore可以理解为是一个字节数组的增强版，是新版本Lucene对current数组的优化，当构建的FST对象大于1GB的时候就会使用BytesStore可以理解为是一个字节数组的增强版对象来存储，否则使用current数组。那么什么时机才是“Compiled”这个动作最好的时机呢？也就是什么时候才是我们从CompiledNode数组中摘下来节点并且计算结果存放在current中的最好时机呢？当然就是等当前节点不会再发生任何变化的时候，因为只有当节点的所有属性都不再发生改变的时候，记录它的描述才是有意义的。那什么时候才能确定它不再会发生改变了呢？以图4-1中的Term Dictionary为例，FST的构造器Builder会在输入第一个term的时候在其构造函数中创建一个长度为10的默认的frontier数组：
当输入第一个term:abandon的时候，在frontier中“挂载”了8个UnCompiledNode和对应的7个Arc的信息，此时并没有任何Node和Arc被写入current[]，因为现在并不能确定任何节点将来是否会发生改变，换句话说，现在还无法确定后面是否有“a”、“ab”、“aba”、“aban”、“aband”、“abando”、“abandon”其中任何一个为前缀的词项，因为下一个term没有输入，它有可能是ac，如果是ac那么Arc a（这里指的是abandon的第一个字符a）对应的节点就产生了第二个出度，也就是发生了变化。注意Arc a对应的节点不是Arc a的target节点，而是a前面的节点，即Arc a是其对应节点的出度；同理，下一个Term也可能是abb，此时Arc a就未发生变化，而是Arc b产生了变化，新增了第二个出度b；当然也可能是abandonment，此时第一个term的终止节点n发生了变化，因为原本n的出度为0，但是现在为1，即Arc m，因此我们在下一个term输入之前，无法确定当前term未来将会发生何种变化。
我们仍然以图4-1中的Term Dictionary为例，当第三个term:abbreviation输入的时候，就可以确定以后不再会有以aba为前缀的term了，因为所有的词项都是按照字典序排列的，当第三个字符出现b的时候，就意味着aba前缀的完结，也就是说此时abandom中的第四个节点S-a也就是Arc a（abandon中的第三个字符）的target节点不再会发生任何改变了，这里需要注意，Arc a对应的节点目前仍不能确定在未来是否会发生改变，因为其对应的节点是S-b也就是Arc b的target节点，后面还有可能会出现以“abc”、“abd”等为前缀的term，因此当前只能冻结节点s-a也就是frontier中的第四个节点。
刚才所描述的这个确定节点不再会发生改变的过程就叫做尾部冻结（freezeTail），freezeTail的实现如下：
再回到图6-1的例子中来，假设输入的第二个term是“abe”，此时如图6-2所示。图中浅粉色节点表示S_e是新加入frontier数组的节点，蓝色加粗边框表示节点S_d是被执行了freezeTail操作，成为了一个CompiledNode。
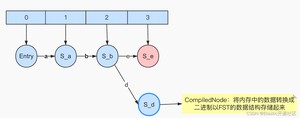
理解FST在Lucene中的构建原理，我们还需要知道什么是PendingBlock和PendingTerm。这两个对象是Lucene在Node的基础上抽象出的两个概念，他们同时继承自PendingEntry。其代码实现如下：
为了弄清楚这两个对象的含义，我们借助下面这张图来帮助我们辅助理解，需要注意，这张图仅仅是为了帮助我们理解几个概念，此图并非FST的原理图。
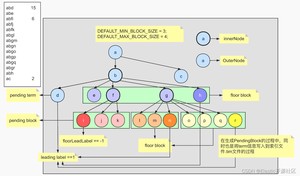
假设上图中树形结构描述的是左侧的Term Dictionary，当节点的子节点的数量不止一个的时候，它可能就是一个Block。比如我们暂时就可以把图中的a、b、f、g都可以看成是Block。关于Block的理解，可以参考本章图2-2中对Block的解释。从图中可以清楚的看到，节点a、b、f、g都包含至少2个或以上的子节点，所以暂时可以把它们看成是一个block。但是在org.apache.lucene.codecs.blocktree.BlockTreeTermsWriter中的writeBlocks方法有这么一段代码：
在这段代码中的英文注释，大概含义是说：如果一个Block太大，也就是子节点过多，Lucene就会把它划分成多个floor blocks（层级块），并且把每个floor block中的第一个字符记做leading label，目的是为了floor block的快速定位。并且在floor block分块的时候，使用了贪婪计数的法则，当block满足至少包含minItemsInBlock个entry信息的时候，才会生成一个block，这种规则通常会导致最后一个block中包含的entry的数量最少。
具体floor是如何划分的？BlockTreeTermsWriter类中定义了两个final类型的静态成员：DEFAULT_MIN_BLOCK_SIZE和DEFAULT_MAX_BLOCK_SIZE。
这里min值和max值分别代表划分floor时满足条件的最小和最大的临界值，其关系是 max <= 2 * (min -1)。也就是说，当block节点的子节点count >= DEFAULT_MIN_BLOCK_SIZE的时候，才会被划分floor block，否则就是pending term，但是当floor count的节点数继续增加到DEFAULT_MAX_BLOCK_SIZE的时候就会被截断，也就是floor block节点的最大值就是DEFAULT_MAX_BLOCK_SIZE，当超过这个临界值的时候，就会被划分成多个floor block或者pending term。如果block的subIndices数量大于等于DEFAULT_MIN_BLOCK_SIZE且小于等于DEFAULT_MAX_BLOCK_SIZE的时候，Block不会被拆分，此时Block称之为Pending Block。其实现如下：
在图6-3中，为了方便演示和读者理解，我暂且把DEFAULT_MIN_BLOCK_SIZE和DEFAULT_MAX_BLOCK_SIZE的值分别设置为3和4，即min=3，max=4。图中豆沙色矩形标注的部分即block的entry。
接下来，我们来演示一下Lucene是如何将Term Dictionary构建成为一个FST对象的。
图6-2中当term:abe输入完成之后生成的数据模型如图6-4所示
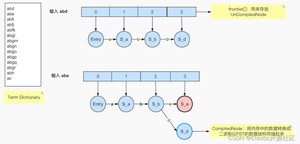
我们继续上图中的过程，并且以图中左侧的Term Dictionary为例，当第三个term:abfi输入的时候，就意味着以“abe”为前缀的所有term都已经结束，当term:abfj输入，意味着所有以“abfj”为前缀的term结束，以此类推，当输入term:abfk之后，frontier如图6-5所示
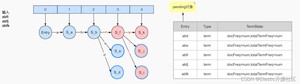
图中蓝色边框的节点代表当前节点已执行freezeTail，被冻结的节点将会从frontier中“摘”下来，此时尚无任何节点数据写入current数组，因为虽然有节点被冻结，但是被冻结的节点都没有任何出度，即 lastFrozenNode = -1，此时pending对象中保存的结构如图右侧所示。
输入term:abgl，此时以“abf”为前缀的所有term都已经结束，此时Arc f的target节点S-f就可以确定不再会发生任何变化，即包括其子节点在内都不会再产生新的出度，此时调用writeBlocks方法将S-f生产Block，因为节点S-f的出度节点数量为3，大于等于min值小于max值，因此生成pending block，如图6-6所示：
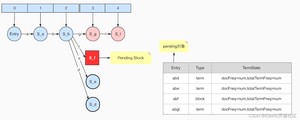
后面的几步执行过程都是相似的，这里不再赘述，当输入term:abh的时候，节点S-g确定不再发生任何改变，冻结尾部执行writeBlocks生成block。由于S-g的出度包含’l‘、’m‘、’n‘、’o‘、’p‘、’q‘、’r‘，由于所有节点冻结都是从尾部开始的，遵循floor block的规则，生成S-p和S-l两个floor block，并最终生成Block：S-g，此时pending对象中已经包含了两个pending block和三个pending term，如图6-7所示：
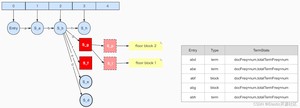
接下来的步骤都是相同的道理了，但是当最后一个term:ac输入之后，因为没有下一个term了，因此所有的节点都已经确认，最终生成的结果如下图6-8所示
数据会最终被全完成frontier数组中摘出来生成byte数组保存在current数组中写入磁盘。
本节我们通过源码来分析一下Lucene是如何把Term Dictionary构建为FST并且保存在BytesStore对象里的。之前我们提过，Lucene在使用Builder构建FST的过程中，创建了以下几个类型或对象：
- UnCompiledNode：保存挂起的节点，尚未serialized的节点。
- CompiledNode：当Node的出度信息完全写入到BytesStore/current数组之后，Node会从frontier中摘下，状态变为CompiledNode。例如在图6-1的时候，输入term:abd，此时生成了四个UnCompiledNode对象以及三个Arc对象，其代码定义如下：
由此我们可以看出，每个UnCompiledNode包含若干个Arc，并且用output表示点解节点的输出值，isFinal表示当前是否是终止节点。
- UnCompiledNode[] frontier：用来存放UnCompiledNode，待处理的节点Arc
- BytesStore bytes（current[]）：存储CompiledNode出度Arc的二进制数组对象。
- Arc：描述FST构建的重要类型，其中我们要着重理解的包括label、output、target和flags四个属性，其他属性我这里都已经做了详细的中文注释，这里我们来把刚才说的四个属性重点讲解一下。
- label：描述当前输入词项中的一个字符，FST最终存储的是label对应字符的ASCLL的二进制。
- output：存储Arc对象的附加值或者叫做输出值，output和finalOutput都属于output。
- target：如果当前的祖父不是输入值的最后一个字符，target会存储当前字符的下一个字符在current数组中的flag值在current数组中的index即索引值。
- flags：通用最小化算法要求任何对数据的压缩都要可以逆向运算，即数据可编码解码，因此在对于FST进行压缩的时候，flags的作用是以最小的代价标记若干个状态值，这里采用了一种位移算法，以实现其通用最小化的目的。
这里label和output都很容易理解，但是target和flags相对难以理解。target的含义我们在FST的写入过程中给大家做详细介绍，但是这flags的含义我们有必要在这里展开来详细的讲解一下。 - lastFrozenNode：当节点从frontier[]数组中摘下来的时候，节点和它包含的Arcs信息会被写入到current[]数组中，lastFrozenNode会记录当前被处理的节点的第一个Arc在current数组中的起始坐标，即flag的坐标。如果当前节点是终止节点，因为终止节点没有出度Arc，因此lastFrozenNode会输出-1。当lastFrozenNode的值和当前处理的Arc指向的target node在current数组的起始坐标不相同并且当前处理的Arc的target node不是Stop node（因为没有出度Arc）的时候，也就意味着最终构建的FST对象存储的current[]数组在读取的时候，当前Arc对应的label在数组中的下一个Arc不是当前term的下一个label，就需要记录当前Arc的下一个Arc在current数组中的坐标，此时flag就不会标记BIT_TARGET_NEXT值。这段描述需要读者多加揣摩和理解。
首先我们先看一下flags在Lucene-FST中的使用场景：
我上面已经提过，flags是用来记录状态值的，但是这里不难发现，flags符合某种状态条件的时候，使用了”+=“这种操作，难道状态也可以累加吗？没错，的确可以，那到底是如何做到呢？我们先看一下flags累加的这几种状态的定义：
在源码中我们可以清楚的看到，flags的累加值一共有六种，分别是1 << 0、1 << 1、1 << 2、1 << 3、1 << 4、1 << 5。<<代表位移方向，后面数字代表位移的bit数。比如1<<1代表十进制1转换二进制之后每个bit位左移一个bit位。Lucene-FST中的flags使用了一个Byte来存储，1的二进制就是0 0 0 0 0 0 0 1，左移一位就是0 0 0 0 0 0 1 0，十进制就是2，以此方式计算，flags做＋=运算的结果，有且仅有一种flags的组合，也就达到了以最小代价存储多个状态信息的目的。当前六个flags的值和其所对应的状态含义如下表：
到这里，几个Lucene中构建FST的几个重要的对象都已经做了响应的介绍，下面来详细介绍一下构建的具体过程。
首先创建Builder对象，BytesStore bytes，并写入一个0，用来标记FST的结束（读取的时候是反向的）。同时初始化一个长度为10的UnCompiledNode[] frontier。Builder对象会在每次输入的时候，调用add(IntsRef input, T output)方法，其主要包含四个步骤：
- 计算当前输入term与上一个term的公共前缀，公共前缀最终指向的节点暂且叫做公共节点。
- 调用freezeTail方法，从尾部开始到公共节点为止，冻结所有已经确定状态的节点，UnCompiledNode状态变为CompiledNode。将已冻结节点的出度和节点信息写入BytesStore或者current[]中，最后更新lastFrozenNode。
- 将当前输入写入frontier[]数组中，把对应信息写入Arc对象，Node的状态为UnCompiledNode。
- 调整当前输入对应Arc的output值。
我们以为例，结合Lucene源码来演示一下FST的存储过程。
1：首先输入term:ab
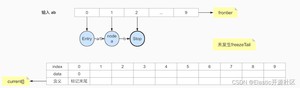
此时由于ab为第一个term，未发生任何节点冻结，因此开始执行第二个term输入，如上图7-2所示
2：因此开始执行第二个 term:abd 的输入
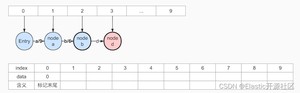
此时公共前缀为“ab”，虽然node a和node b都是终止节点，但是无法确定其是否会发生改变（即新增出度或者target节点，因为还有可能会有以ab或者abd为前缀的term调add添加进来），所以未发生freezeTail。终止节点没有出度，即不包含Arc，返回-1，lastFrozenNode=-1）。将节点arc：d对应节点node d写入frontier数组中。15（9+6）>9，取公共部分9 => 最小法则 目的是生成最小化FST，这个也是遵循数据结构的通用最小化算法法则。
3：输入term:abgl，如图7-4所示：
公共前缀：term:ab，freezeTail：arc:d=>node d(终止节点，不会发生改变了，lastFrozenNode=-1)，同样，node b和node l 都无法确定是否还会有变化，即无法确定后面是否还有以ab或abgl为前缀的term，将arc g、arc l对应节点node g和node l 写入frontier数组中，15（9+6）>9，取公共部分9 => 最小靠前法则 目的是生成最小化FST，这个也是遵循数据结构的通用最小化算法法则。
此时Arc-d并未马上写入current[]的bytes对象中，因为出度d的target虽然是node d但它是node b的出度，只有当node b被冻结的时候，node b的所有出度才会被写入字节数组。换句话说，判断一个Arc写入current字节数组的时机，就是出度对应的node的所有（最后一个）出度确定的时候。
4：输入term:acd，如图7-5：
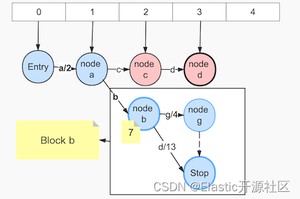
此时公共前缀为’a’，调用freezeTail冻结了Step 3中的node b、node d、node g、node l，出度分别是Arc-d Arc-g Arc-l，要注意这里的Arc-b必须要在node a的最后一个出度确定之后才能处理，显然这里不能确定Arc-c就是node a的最后一个出度，因为只要还有以’a’开头的term，node a就可能还有新的出度。将节点Arc：d对应节点node d写入frontier数组中。最后更新output，逻辑同上。
处理顺序：节点从后往前，Stop Node => node g（arc：l）=> node b（arc：d、g）
1：处理Stop node：
2：处理node g：
Current[] 如下表所示：
3：处理node b
上图7-7为将node n的Arcs信息写入current[]数组后的结果，此时node b的其实位置为Arc d的起始位置，即d的flag坐标：8，因此lastFrozenNode此时会被更新为8，即：lastFrozenNode = 8。
这里需要注意，我在描述lastFrozenNode的概念的时候说过，当前处理的Arc d指向的节点在current数组中的起始位置和astFrozenNode的值不相同的时候并且Arc d指向的节点不是Stop node的时候，需要记录当前Arc的下一个Arc（按照label在term中的顺序）在current数组中的坐标：target index，但是当前处理的Arc d指向的节点是Stop node，因此也就不必记录target index。
5：输入term:msbc，如图7-8：
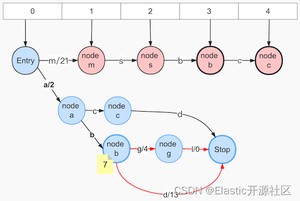
此时，Entry节点产生了第二个出度，调用freezeTail方法冻结了Step 4中的node a、node c（这里指的是图中蓝色的node c）、node d，出度分别是Arc-c Arc-d，要注意这里的Arc-c可以确定是node a的最后一个出度，所以node a后面的所有Arc将开始处理。同样m无法确定是entry的最后一个出度，所以 Arc a不能处理。图中红色的出度标示之前已经被处理。
处理顺序：节点从后往前，Stop Node => node c（arc：d）=> node a（arc：b、c）
1：处理Stop node：返回 lastFrozenNode = -1
2：处理node c：
3.处理node a
注意：当前的lastFrozenNode是node c产生的，b指向的node b而非node c，并且node b不是Stop node，此时需要记录Arc b的target index值，即node的第一个出度在current[]数组中的起始位置，即：
8，最终结果如下图7-10所示：
6.输入term:mst，如图7-11：
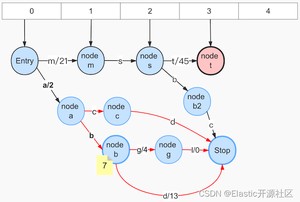
此时，公共前缀为"ms"，调用freezeTail方法冻结了Step 5中的node b2和node c，此时node s的出度Arc b并不会写入current，因为node s的尚未确定所有出度，但是nodeb2后面的出度是可以写入字节数组的，因为node b2的所有出度都已经确认了
处理顺序：节点从后往前，Stop Node => node b2（arc：c）
1：处理Stop node：
2：处理node b2：
处理完成之后current[]如下图：
7.输入term:wl，如下图7-13：
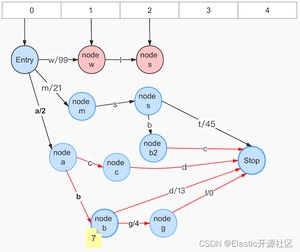
此时，公共前缀为：ms，调用freezeTail方法冻结了Step 6中的node s和node m。
处理顺序：节点从后往前，Stop Node => node s（arc：b、t）=> node m（arc：s）
1：处理Stop node：
2：处理node s：
3：处理node m：
处理完成之后current[]如下图7-14：
因为term:wl是Term Dictionary中的最后一个term，所以此时node w和在frontier中的node s（图7-13中红色node s）以及Entry node也都可以确定不会再有新的出度产生，因此会被冻结，即如图7-15所示：
处理顺序：节点从后往前，Stop Node => node w（arc：l）=> Entry node（arc：w、m、a）
1：处理Stop node：
2：处理node w：
3：处理Entry node
处理完成之后current[]如下图7-16：
此时完整的FST对象已经构建完毕并写入current[]数组，图中展示的为十进制数字是为了方便读者理解，实际存储的完全为二进制。
下面是如何从current中读取完整的Term Dictionary：
读取操作是从后往前的，即：
- 从index:39开始，此时key = ‘a’，当读到index : 36，此时target index指向16，index : 16的位置存储的label为’b’，此时key = “ab”，final output = 7即可判断当前为终止节点，这里就不用计算flags了，即此时读取到term:ab，此时Term Dictionary中包含一个term:ab，value = 2+7，即：term:ab/9。
- 由于index : 16中index指向index : 8，此时key = abd，flags = 27，27有唯一的flag组合：16 + 8 + 2 + 1，即BIT_ARC_HAS_OUTPUT、BIT_STOP_NODE、BIT_LAST_ARC、BIT_FINAL_ARC的组合，由BIT_STOP_NODE可得当前是终止节点，所以此时读取到term:abd，value = 2 + 13 = 15 ，即：term:abd/15。此时Term Dictionary中包含两个元素：term:ab/9、term:abd/15。
- 由于index : 8的Arc d没有target index，因此继续沿着数组往下读，即读取index : 5，即Arc g，通过前面的flags值计算可得此时key = “abg”， Arc g仍然没有target index，因此继续读取index : 2，同理可得此时key = “abgl”，继续读或者通过flags都可以判断当前是一个终止节点，所以此时得到term:abgl，value = 2 + 4 = 6，即term:abgl/6。此时Term Dictionary中包含三个元素：term:ab/9、term:abd/15、term:abgl/6。
- 此时node a的第一个出度Arc b已经遍历完毕，即index : 16后面的数据已经读取完毕，此时读取’b’在current数组中的顺序数据，即index : 12，原理同上，读至index : 10，由flags可得当前为终止节点，此时得到term:acd/2。此时Term Dictionary中包含四个元素：term:ab/9、term:abd/15、term:abgl/6、term:acd/2。
- 此时Entry的第一个出度Arc a的所有信息都已经遍历完成，即index : 39的target index后面的数据以及读取完毕，按照current数组顺序读取至index : 35，根据其target index : 26读取到Arc s，顺序读至index : 24，根据其target index读至index : 18，再根据当前Arc c的flag的到term:msbc，value = 21。即：term:msbc/21。此时Term Dictionary中包含五个元素：term:ab/9、term:abd/15、term:abgl/6、term:acd/2、term:msbc/21。
- 此时node s的第一个出度Arc b遍历完毕，沿着Arc b顺序读取至index : 21，计算flags可得当前节点为Stop node，即得到term:mst，value = 21 + 45 = 66，即term:mst/66。此时Term Dictionary中包含六个元素：term:ab/9、term:abd/15、term:abgl/6、term:acd/2、term:msbc/21、term:mst/66。
- 此时Entry的第二个出度Arc m的所有信息已经读取完毕，沿着index : 35继续往后顺序读取，读取index : 31，然后顺序读取至index : 28，通过计算flags可得当前节点为终止节点，即得到term:wl，value = 99，即term:wl/99，此时Term Dictionary中包含七个元素：term:ab/9、term:abd/15、term:abgl/6、term:acd/2、term:msbc/21、term:mst/66、term:wl/99。
至此，已经完成了对current[]数组的数据读取并还原了Term Dictionary的数据。
以上为博主结合Lucene以及ES源码整理的倒排索引相关底层的解读，如有任何疑问或错误欢迎交流和指正。
版权声明：
本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。
本文网址：https://www.mushiming.com/mjsbk/11122.html