目录
一、什么是二叉树?
二、二叉树的遍历
1. 先序遍历
2. 中序遍历
3.后序遍历
4. 遍历的推导
三、重要的事情
1. 二叉树:一种树形结构,特点是每个结点至多只有两颗子树,并且子树有左右之分,次序不能颠倒。
特殊形态的二叉树:满二叉树和完全二叉树;
2. 满二叉树:最后一层都是叶子结点,每个结点都是满的(每结点都有两颗子树)。
3. 完全二叉树:有n个结点,且符合满二叉树的编号次序。
- 先序遍历 DLR (依次遍历:根结点,左子树,右子树)
- 中序遍历 LDR (依次遍历:左子树,根结点,右子树)
- 后序遍历 LRD (依次遍历:左子树,右子树,根结点)
看不懂?不急,直接上图。(二叉树就像递归一样,一层一层的。)
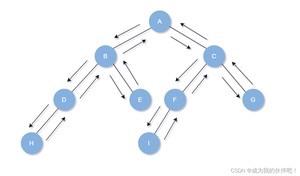
从根结点开始围着跑,依次写出即可。(这是简单的方法,也是最快的,但还是要看一下下面的详细解释哦)
图中序列为:A B D H E C F I G
详细解释(我称它为"三分法"):先序遍历是先根,再左,后右,像递归一样一层一层拨开,(此处的根结点是每一个结点皆可是根,而不是最顶上的根结点),如下图;分好根左右后,按我们上面的定义(依次遍历:根结点,左子树,右子树)
根是A(写下来),再拨左子树,此时左子树可分成图二;根是B(写下来),再拨左子树,又拨成图三的样子;根是D(写下来),拨不下去了,回到根是D的情况,在图三中,H成为了左子树(写下来),发现没有右子树,那就不写了;回到根是B的情况,在图二中,根结点和左子树已经被我们写好了,到右子树了,右子树是E(写下来);如此如此,这般这般,再按此方法把图一中的右子树划分成图四,图五的样子,剩下的交给你了。写出来为:A B D H E C F I G
图中序列为:H D B E A I F C G
404???!!!
嘻嘻,这次没有快捷办法了!但按我上图的"三分法"敲好用。(熟练后心中直接出图,不用像我一样框出来)
解释:不要忘了定义:中序遍历 LDR (依次遍历:左子树--->根结点--->右子树)
图一中根是A,但我们要先写左子树,开始拨图二,发现还有,继续拨它;图三中,左子树是H(写下来),根是D(写下来),右子树,没有就不写;回到图二,根是B(写下来)因为左子树已经被我们写好了,右子树是E(写下来);回到图一,根是A(写下来),开始写右子树,然后就是图四,图五了;交给你了,别忘了定义!定义!定义!写出来为:H D B E A I F C G
图中序列为:H D E B I F G C A
目前还是没有发现又快又保证能对的方法,但"三分法"依旧很强,熟练后就又快又准了。
解释:后序遍历 LRD (依次遍历:左子树,右子树,根结点)
先左子树,我们一眼拨到图三,左子树H(写下来),没有右子树,那就到根D(写下来)了;图二中,右子树是E(写下来),根是B(写下来);拨到图五,左子树是I(写下来),F(写下来)是根;图四,右子树是G(写下来),根是C(写下来),最后A是图一的根;写出来为:H D E B I F G C A
如下面的题。PS:如果只给 前序遍历序列和后序遍历序列 是不能确定唯一二叉树的(判断题)。

简单的方法:后序遍历最后一个序列结点一定是最顶上的根结点,先序遍历第一个序列结点一定是根结点。所以此题只能含泪选D再拿3分了。
开玩笑,要是换个干扰项怎么办呢?还是要有真功夫的!
解释:后序可判断C为根结点,这样从(1)可推出左子树,大家可还记得上面图四和图二的后序遍历吗?看看他们各自的根结点与总结点A有上面关系?你试着画一个没有右子树的,看看它的后序遍历是什么。这样由后序(2)可推E为根,由中序可推左右子树,(5)再推根,又可中序推出左右子树,这样图5.2就画出来了。中序判左右,后序判根结点。再看下一题巩固下。
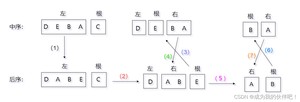
别急着看结果,自己画一下

此题为:D
详细解释:由先序遍历推出根结点为A,由(1)可推左子树为DGB,右子树为ECHF;由(2)可确定左子树的根为B;根为B,由(3)可推知DG为左子树,再由(4)知D为根,由(5)可推G为右子树;这样就可以画出左边的图了(例图三)。ECHF交给你们了,请用好我的“三分法”哦!结果为(例图四);由先序推根,中序推左右子树。
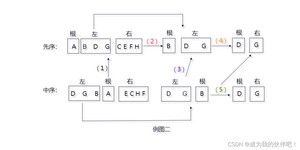
自己画一下
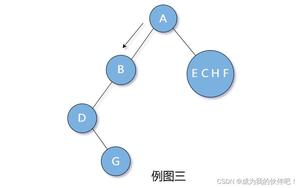
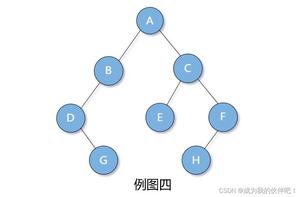
根左右,左根右,左右根 三者相互限制可判断出相应位置。
感觉不错的话,就请点赞支持一下吧!纯手工打造哦!谢谢!!!
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/11868.html
