对于图结构来说,图的遍历和树的遍历有类似之处,树结构的遍历从根结点出发,图结构的遍历从某一结点出发。出发之后,按照某种手法无重复地访问所有的结点,这也是后续解决图的连通性、拓扑排序和关键路径的预备知识。
由于在图结构中,任意顶点都有可能与其他顶点相互邻接,因此如果没有对已走过的路径进行记录的话,很有可能会由于结点的重复访问而无法遍历所有顶点。因此我们需要一种手法记录访问过的顶点,一种直接而有效的手法是使用一个 visited[n] 数组,先将其每一个元素初始化为 0,当我访问了第 i 个顶点时,就将 visited[i] 的值赋值为 1,表示已经访问过。当我访问某一个顶点时,可以通过 visited 数组来确定我接下来是否要从这个顶点往下走。
深度优先搜索( Depth First Serarch )我们之前是接触过的,在迷宫问题(栈实现)和树结构的递归遍历法中,我们用其思想实现了一些功能,现在我们来详细谈一谈。所谓 DFS,我称之为视角放在路径的手法,思想是通过对某一条路径的顶点的挖掘,从而试探出一条可行的路径。当我使用递归或者通过修饰后的栈结构,可以实现回溯的效果,以获取全部的路径。
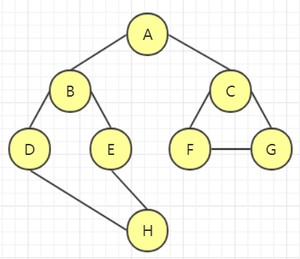
对于一个连通图,DFS 的遍历过程为:
- 选择图中的某个顶点出发,并访问该顶点;
- 找出刚访问过的顶点的第一个未被访问的邻接点并访问;
- 以该顶点为新顶点,步骤 2 直至刚访问过的顶点没有未被访问的邻接点;
- 返回前一个访问过的且仍有未被访问的邻接点的顶点,找出该顶点的下一个未被访问的邻接点,并访问该顶点;
- 重复上述 2、3、4 步骤直至所有顶点访问完毕。
例如上图的连通图,我们选择顶点 A 出发,访问该顶点:
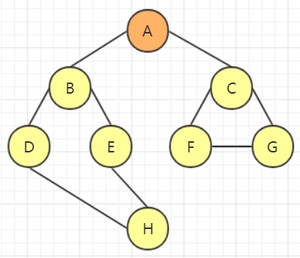
选取 A 的邻接点 B,访问该结点:
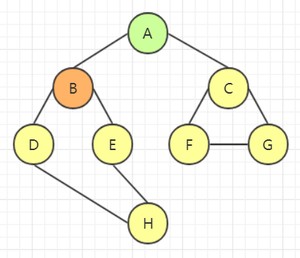
选取 B 的邻接点 D,访问该结点:
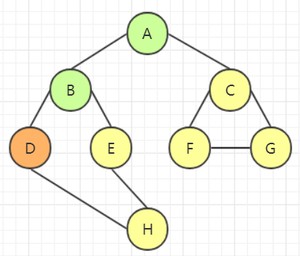
选取 D 的邻接点 H,访问该结点:
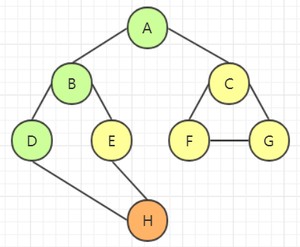
选取 H 的邻接点 E,访问该结点:
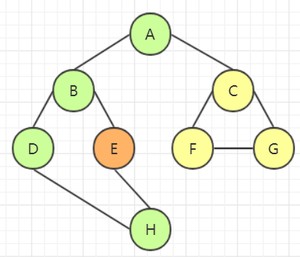
由于 E 顶点的所有邻接点都遍历完了,因此需要回溯。回溯需要 4 次回到顶点 A,并访问下一个邻接点 C:
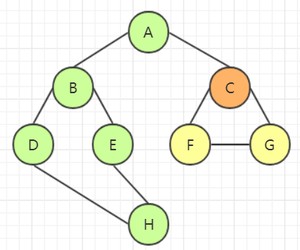
选取 C 的邻接点 F,访问该结点:
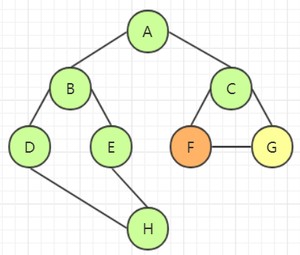
选取 F 的邻接点 G,访问该结点:
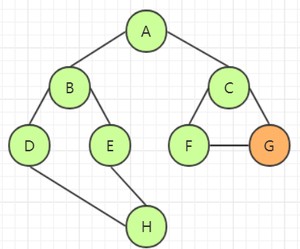
遍历完毕,顺序为 A->B->D->H->E->C->F->G。其深度优先生成树为:
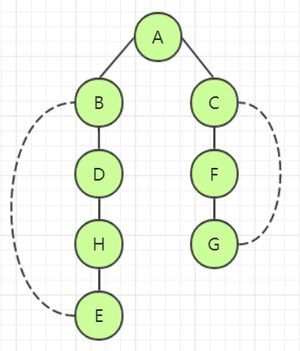
由于 DFS 需要涉及到回溯问题,因此我们想到使用递归来实现。
当我们遍历一个连通图时,对图中每个顶点至多调用一次 DFS 函数,并且当这个顶点被访问过之后,由于被标志成已被访问,就不再从它出发进行搜索。因此,遍历图的过程实质上是对每个顶点查找其邻接点的过程,其时间复杂度则取决于使用的存储结构。当用邻接矩阵描述图结构时,查找每个顶点的邻接点的时间复杂度为 O(n2),其中 n 为图结构中的顶点数。当以邻接表做图的存储结构时,查找邻接点的时间复杂度为 O(e),e 为图结构的边数。由此当以邻接表做存储结构时,深度优先搜索遍历图的时间复杂度为 O(n + e)。
广度优先搜索( Breadth First Serarch )我们之前也有接触过,在迷宫问题(队列实现)和树结构的层序遍历法中,我们用其思想实现了一些功能,现在我们来详细谈一谈。所谓 BFS,我称之为视角放在整个图结构的手法,思想是通过从某个顶点向外扩散,从而囊括所有顶点的手法。当我借助队列结构时,可以实现该算法。
对于一个连通图,DFS 的遍历过程为:
- 选择图中的某个顶点出发,并访问该顶点;
- 依次访问 v 的每个未曾访问过的邻接点 i;
- 分别从这些邻接点出发,依次访问它们的邻接点,并使“先被访问的顶点的邻接点”先于“后被访问的顶点的邻接点”被访问;
- 重复步骤 3,直至图中所有己被访问的顶点的邻接点全部访问到。
例如上图的连通图,我们选择顶点 A 出发,访问该顶点:

访问顶点 A 的所有邻接点:
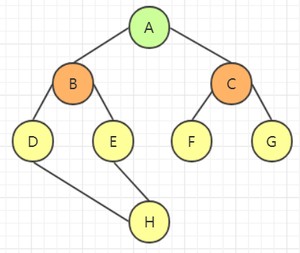
访问顶点 B 的所有邻接点:
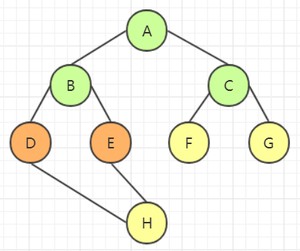
访问顶点 C 的所有邻接点:
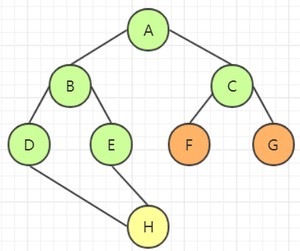
访问顶点 D 的所有邻接点:
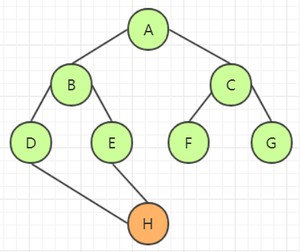
接着访问剩下的顶点,由于所有的顶点都被访问过了,因此没有新顶点入队列。遍历顺序为:A->B->C->D->E->F->G,广度优先生成树为:
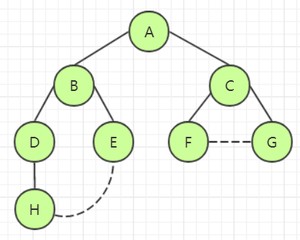
对于 BFS,每个顶点至多进一次队列,因此遍历图的过程实质上是通过边找邻接点的过程。因此广度优先搜索遍历图的时间复杂度和深度优先搜索遍历相同,两种遍历方法的不同之处仅仅在于对顶点访问的顺序不同。
这道题表面上看好像不好懂,但在本质上是一个有限的图结构遍历,即我们可能在遍历到某些顶点的时候就需要提前结束了。基于这一点,我们反应过来用 BFS 做比较方便一点,因为 BFS 的流程可以抽象为一层一层地往外探测,这与我们的思路是符合的。
那么接下来我们读题,根据题意,我们需要找到关系网在 6 层以内的结点。那也就是说,我们需要去记录某个顶点,它对于初始顶点来说是第几层的关系网。为了方便理解,我展示的做法是去修改记录结点信息的数组的结构体为:
即多开一个成员来记录层次的信息。那么层次的信息怎么操作?首先我们先初始化为 0,接下来每进行一轮 BFS,添加入队列的顶点就从它的上一层继承层数,可以用这行代码实现:
解决了层次的确定问题,剩下的就是我们喜闻乐见的建图和遍历的事情啦。

六度空间理论(数学领域的猜想)
左转我另一篇博客——PTA习题解析——判断DFS序列的合法性
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/13378.html
