红黑树是一个接近平衡的二叉查找树,也就是说二叉查找树的特性红黑树应该都具备,那么具备哪些特性呢?
- 左子树小于根节点
- 右子树大于根节点
- 左右子树也分别为二叉查找树
换句话就是有序的。那么有什么优点呢?
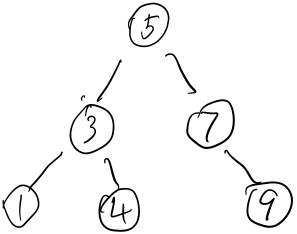
比如我要插入2,该怎么插入呢?
和5比较,<5,到左侧;和3比较,<3到左侧;和1比较,>1,到1的右侧;
比如查询1呢?该如何查询?其实一思考,查询的过程和插入的过程是一样的,其实也就是二分查找的思想。所查询的次数也就是树的高度。其时间复杂度为logn.
那问题来了,什么是红黑树呢?我们如上举例是一个平衡的二叉树,因为根节点是5。但是当有一个诸如这样的序列:1,4,5,7,8,9那么这个二叉树会变成什么样?
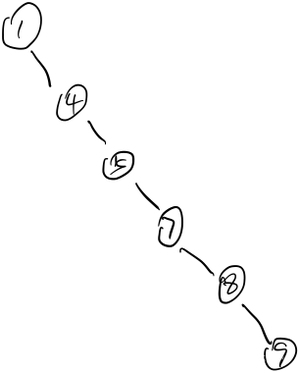
那么时间复杂度就变成了O(N),当数据量足够大的情况下,那速度就可想而知。
所以我们便衍生出了红黑树,一个自平衡的二叉树,除了具备二叉树的特性,还具备以下特性:
- 每个结点不是红色就是黑色
- 不可能有两个红色结点相连,每个叶子都是空的黑结点(null),不存储数据
- 根节点都是黑色root
- 每个结点,从该结点到其可达叶子结点的所有路径,都包含相同数目的黑色结点
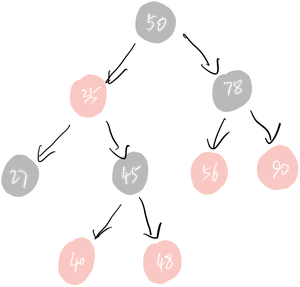
当插入或者删除的时候,红黑树的规则可能就会被打破,那么就得做出一些调整,去维持这些规则。
要求:
- 父节点是红色;
- 叔父节点也是红色;
变更:
- 将父节点和叔父节点变为黑色;
- 爷爷节点变为红色;
- 把指针指向爷爷节点,变为下一步要操作的结点;
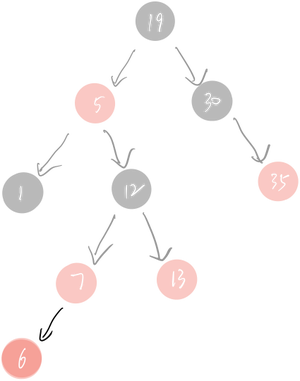
6是想要插入的数值,发现父和叔节点都是红色,则采用变色处理:
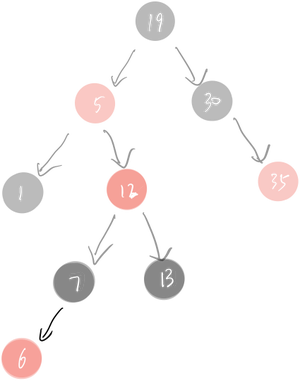
要求:
- 当前父节点是红色;
- 叔父节点是黑色;
- 当前的结点是右子树;
- 指针变化到父节点(未旋转之前的父节点)
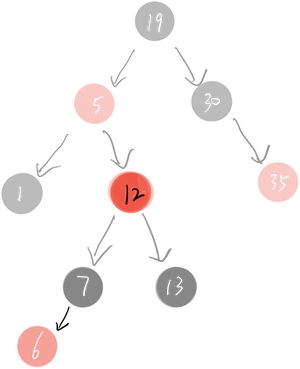
上一步已经把指针指向了爷爷节点,我们发现12这个爷爷节点符合左旋的规则,所以进行左旋。
12的父结点变为自己的左结点,自己的左结点给了父节点作为他的右结点。如下图:

要求
- 当前父节点是红色;
- 叔父节点是黑色;
- 当前的结点是左子树;
- 以爷爷节点右旋;
变更
- 父节点变为黑色;
- 爷爷变为红色;
如上例子还未到平衡二叉树,左旋完成之后,将结点指向了操作结点5。5的父节点是红色,叔父节点是黑色,且5是左子树,满足右旋,将爷爷节点变为红色,父节点变为红色,移动位置,如下图:

如上则完成了红黑树的要求。整个变更流程如下图,
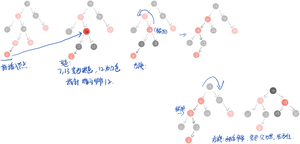
分析下来,通过插入一个节点对于红黑树的基本操作有了一个基本的了解。所以其时间复杂度都是接近于logn。
最熟悉的用红黑树的地方就是jdk8对应的hashmap,红黑树其实也是采用的二分法,相比于二叉查找树,可以避免单一链表,腿脚部分的特殊情况的出现。最坏的情况,时间复杂度也就是接近logn。同样的道理,这也是为何不用数组+链表,而又加入了红黑树的原因,也是为了避免链表过长,降低了效率。那为何不直接用红黑树呢?还得加上链表?因为红黑树需要进行左旋,右旋操作, 而单链表不需要。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/13819.html
