径向基函数是某种沿径向对称的标量函数,通常定义为样本到数据中心之间径向距离(通常是欧氏距离)的单调函数(由于距离是径向同性的)。
理解RBF网络的工作原理可从两种不同的观点出发:
(1)当用RBF网络解决非线性映射问题时,用函数逼近与内插的观点来解释,对于其中存在的不适定(参考中有讲解)问题,可用正则化理论来解决;
(2)当用RBF网络解决复杂的模式分类任务时,用模式可分性观点来理解比较方便,其潜在合理性基于Cover(参考中有讲解)关于模式可分的定理。下面阐述基于函数逼近与内插观点的工作原理。
1963年Davis提出高维空间的多变量插值理论。径向基函数技术则是20世纪80年代后期,Powell在解决“多变量有限点严格(精确)插值问题”时引人的,目前径向基函数已成为数值分析研究中的一个重要领域。
考虑一个由N维输人空间到一维输出空间的映射。设N维空间有P个输人向量,P=1,2,…,P,它们在输出空间相应的目标值为d^p,p=1,2,…,P,P对输入输出样本构成了训练样本集。插值的目的是寻找一个非线性映射函数F(X),使其满足下述插值条件:
(1)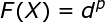
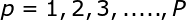
函数F描述了一个插值曲面,所谓严格插值或精确插值,是一种完全内插,即该插值曲面必须通过所有训练数据点。
采用径向基函数技术解决插值问题的方法是,选择P个基函数个训练数据,各基函数的形式为:
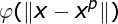
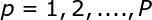
式中,基函数fai为非线性函数,训练数据点xp是fai的中心。基函数以输人空间的点x与中心x^p的距离作为函数的自变量。由于距离是径向同性的,故函数被称为径向基函数。基于径向基函数技术的差值函数定义为基函数的线性组合:
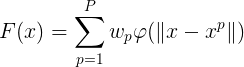
在这里需要解释一下||x-xp||这是范数,在平面几何的向量来说就是模,然而一旦维度很高就不知道是什么东西了,可能是衡量距离的一个东西,那么这个代表什么意思呢?简单来说就是一个圆而已,在二维平面,x^p就是圆心,x就是数据了,这个数据距离圆心的距离,因为和数据的位置和大小无关,只和到圆心的半径有关,况且同一半径圆上的点到圆心是相等的因此取名为径向,代入映射函数就是径向基函数了,我们看看径向基函数有什么特点:
将(1)式的插值条件代入上式,得到P个关于未知系数w^p,p = 1,2,…,P的线性方程组:
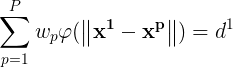
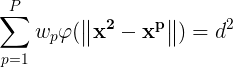
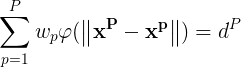
令
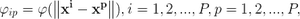
则上述方程组可改写为:(其中第一个矩阵下标存在错误,相信你能看懂)

令大fai表示元素fai ip的PxP阶矩阵,w和d分别表示系数向量和期望输出向量,(5)式还可以写成下面的向量形式:
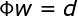
式中,大fai称为插值矩阵,若大fai为可逆矩阵,就可以从(6)式中解出系数向量w,即:
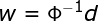
通过上面大家可以看到为了使所有数据都在曲面还需要系数调节,此时求出系数向量就求出了整个的映射函数了。
RBF 和 BP network 区别:
BP神经网络的隐节点采用输入模式与权向量的内积作为激活函数的自变量,而激活函数采用Sigmoid函数。各隐节点对BP网络的输出具有同等地位的影响,因此BP神经网络是对非线性映射的全局逼近。
RBF神经网络的隐节点采用输入模式与中心向量的距离(如欧式距离)作为函数的自变量,并使用径向基函数(如Gaussian函数)作为激活函数。神经元的输入离径向基函数中心越远,神经元的激活程度就越低。RBF网络的输出与数据中心离输入模式较劲的“局部”隐节点关系较大,RBF神经网络因此具有“局部映射”特性。
RBF网络:神经元是一个以gaussian函数(或者其他)为核函数的神经元。
RBF Network 通常只有三层。 输入层、中间层计算输入 x 矢量与样本矢量 c 欧式距离的 Radial Basis Function (RBF) 的值,输出层计算它们的线性组合。
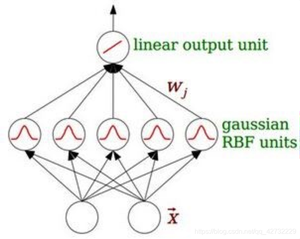
第一阶段为非监督学习,从数据中选取记忆样本。例如聚类算法可在该阶段使用。
第二阶段为监督学习,训练记忆样本与样本输出的联系。该阶段根据需要可使用BP。
隐藏层的作用是把向量从低维映射到高维,低维线性不可分的情况到高维就线性可分了(戳这里理解)。
参考
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/14145.html
