图的遍历是图论中的核心概念,通过不同的遍历方法能够有效地处理多种问题,例如连通性检测、路径查找、图的最小生成树等。本篇我们将重点探讨图的深度优先搜索(DFS)和广度优先搜索(BFS)两种常见的图遍历方法,分析它们的原理、应用场景以及实现方法,并通过实际案例代码分析问题解决方案。

图是一种表示对象间关系的数据结构,由顶点和边组成。按照边的方向,图可以分为有向图和无向图。图的遍历主要有两种方式:
- 深度优先搜索(DFS):优先深入图的分支,直到无法继续时回溯。
- 广度优先搜索(BFS):优先探索与当前节点相邻的节点,然后逐层向外扩展。
无向图示例
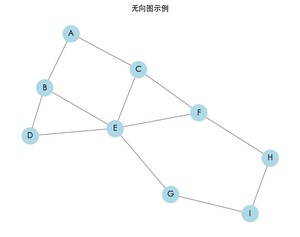
下面是一个无向图示例,适合用于探讨图的遍历(深度优先搜索和广度优先搜索)。
在这个图中,节点的连接关系如下:
- A 连接 B、C
- B 连接 D、E
- C 连接 E、F
- D 连接 E
- E 连接 G、F
- F 连接 H
- G 连接 I
- H 连接 I
绘制图形
下面的代码使用 和 库绘制该图。请确保已安装这两个库(如果尚未安装,请运行 )。
以下是绘制上述无向图的 Python 代码:
运行上述代码将生成一个表示上述无向图的可视化图形,为后续对深度优先搜索(DFS)和广度优先搜索(BFS)的探讨提供一个演示基础。
代码释意
- 导入库:使用 来绘制图形,使用 来处理图结构。
- 创建图:创建一个无向图对象 。
- 添加边:通过 方法将边添加到图中,定义节点之间的连接关系。
- 设置图的布局:使用 选择图形的布局,这有助于更清晰地展示图的结构。
- 绘制图形:使用 来绘制图,设置节点的颜色、大小和标签。
- 显示图:通过 来显示绘制的图形。
基本概念
深度优先搜索利用栈(可以用递归实现)来访问图中的节点。当访问一个节点时,会深度探索该节点的所有相邻节点,直到无法继续。
算法步骤:
- 从起始节点开始,标记为已访问。
- 递归访问未访问的相邻节点。
- 如果所有相邻节点都已访问,回溯到上一个节点。
下面我们将逐步展示如何使用 Python 代码演示无向图的深度优先搜索(DFS)过程与效果吗,并实现 DFS 算法。
可视化 DFS 过程
在实现 DFS 并打印结果后,我们可以通过 绘制这幅图以可视化 DFS 的遍历过程。为了展示仍然在访问中的节点,我们将在访问每个节点时更新图像。
以下是完整的 DFS 过程可视化实现:
代码释意
- 图的构建:使用 方法构建无向图,确保每个节点都相互连接。
- DFS 实现:使用递归方法进行深度优先搜索,同时在每次访问节点时调用可视化函数。
- 可视化函数:使用 不断更新图的显示,以展示各个节点的遍历状态。
- 交互模式:通过开启交互模式(),允许我们逐步更新图。
运行示例
运行上面的完整代码,可以看到图的遍历过程。每次访问一个节点时,节点将会变为橙色,表示已访问。最终,程序也会打印出 DFS 的结果路径。
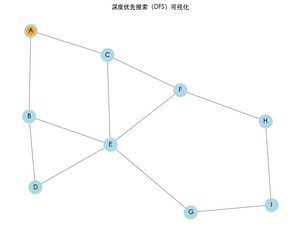
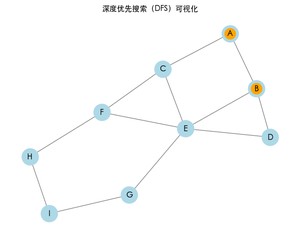
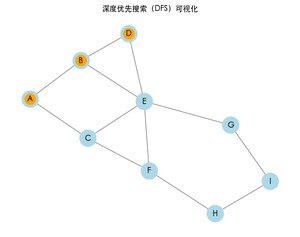
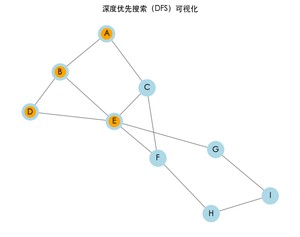
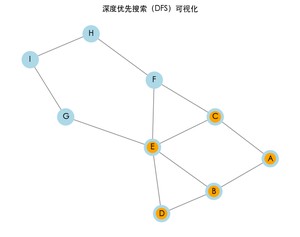
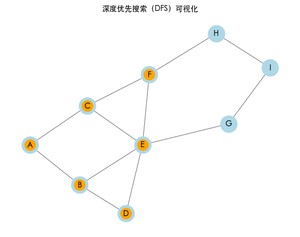
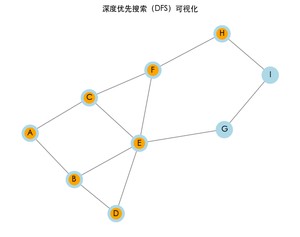
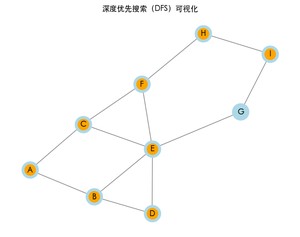
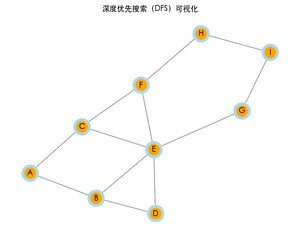
深度优先搜索的结果:
深度优先搜索(DFS)
下面是 DFS 算法的实现。我们使用一个递归方法进行实现,在访问每个节点时记录路径,以便可视化图遍历结果。
关键点
- 递归深度:DFS 的递归深度可能导致栈溢出,特别是在具有深层嵌套的图上。可考虑使用显式栈来替代递归。
- 访问状态:使用集合来管理访问状态,提高查询效率。
DFS 应用场景
- 连通性检测:判断图中是否存在连接路径。
- 图的遍历:访问图中的所有节点。
- 找出图中的环:通过深度优先遍历可以判断图中是否存在环。
- 路径查找:在特定情况下寻找从起点到终点的路径。
基本概念
广度优先搜索利用队列来逐层访问图中的节点。首先访问起始节点,然后将所有直接相邻的节点入队,并继续出队和访问这些节点。
算法步骤:
- 从起始节点开始,将其加入队列并标记为已访问。
- 循环直到队列为空,出队当前节点,并访问其相邻节点。
- 将未访问的相邻节点入队并标记为已访问。
我们逐步展示如何使用 Python 代码演示无向图的广度优先搜索(BFS)过程与效果,以及实现 BFS 算法。
可视化 BFS 过程
以下是使用队列实现 BFS,访问每个节点时记录路径,以及可视化图遍历结果。
代码释意
- Graph 类:
- 使用 创建无向图。
- 方法将边添加到图中。
- 广度优先搜索(BFS):
- 方法使用队列()遍历图。
- 访问每个节点时,将其添加到路径中,并调用 方法进行图的可视化。
- 可视化方法:
- 方法清空图并重新绘制,只标记已访问的节点。
- 使用 使图的更新可见。
运行示例
运行上述代码后,将看到一个窗口,展示 BFS 的遍历过程。每次访问一个节点时,该节点会变为橙色,同时终端将打印 BFS 的结果路径。
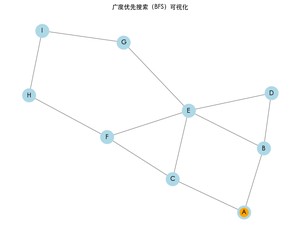
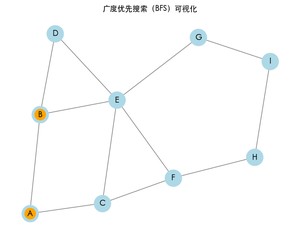
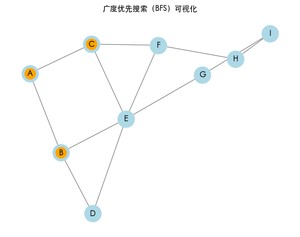
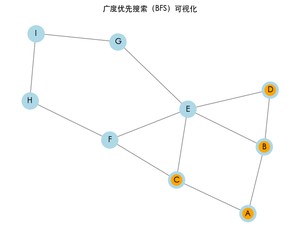
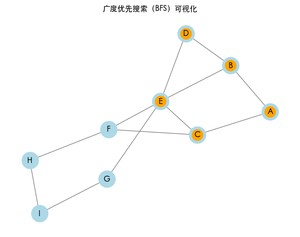
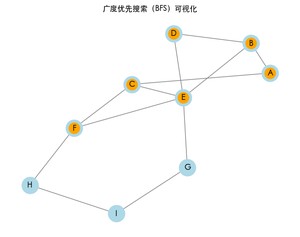
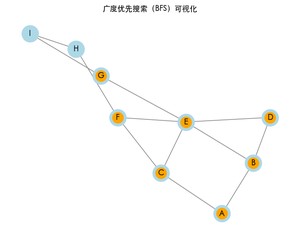
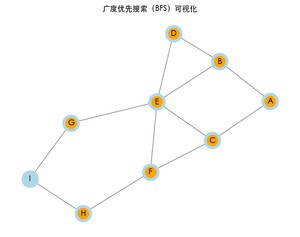
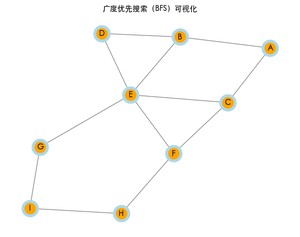
广度优先搜索的结果:
广度优先搜索(BFS)
以下是 BFS 的实现示例:
关键点
- 队列管理:使用双端队列()提高入队和出队效率。
- 内存消耗:BFS 可能在大图上消耗更多的内存,以存储队列和访问状态。
应用场景
- 最短路径查找:在无权图中,BFS 可找到从源节点到其他节点的最短路径。
- 网络广播:在网络中实现信息传播。
- 连通分量的寻找:用于找出不同的连通区域。
深度优先搜索(DFS)和广度优先搜索(BFS)是图遍历的两种基本算法,各自具有独特的特点和应用场景。
基本概念对比
DFS 尽可能深地搜索图的分支,直到该分支末端才会进行回溯。可以基于递归或显式栈来实现。沿着一条路径走到尽头,再回退到最近的分支。
BFS 按层次逐层扩展,同一层的节点会在深入下一层之前全部访问。使用队列来实现。首先访问起点的所有直接邻居,然后依次访问每个邻居的邻居,直到所有节点被访问。
性能对比
- 时间复杂度:
- DFS:$O(V + E) $, 是顶点数, 是边数。
- BFS:,同样的复杂度。
- 空间复杂度:
- DFS:最坏情况下为 , 是树的高度(对于深度较大的图可能会出现栈溢出)。
- BFS:最坏情况下为 ,因为可能需要存储所有节点。
场景分析
深度优先搜索(DFS)
- 应用领域:
- 图的连通性检测:DFS 可以用来检测图是否连通,或找到图的连通分量。
- 路径查找:适合查找从起点到终点的任意路径(不是最短路径)。
- 拓扑排序:在有向无环图(DAG)中进行拓扑排序。
- 拼图游戏:如八数码问题、迷宫求解等可以使用 DFS 来尝试不同路径。
- 场景示例:
- 迷宫探索:在迷宫中寻找一条通向出口的路径,DFS 可以快速深入复杂的路径。
- 网络爬虫:在网页链接中递归访问,直到没有未访问的链接。
广度优先搜索(BFS)
- 应用领域:
- 最短路径查找:BFS 可以在无权图中找到从起点到终点的最短路径。
- 层次遍历:适合在树或图中进行层次遍历,获取节点的层级信息。
- 网络广播:在传播消息或数据时使用 BFS,有助于确保信息的快速扩散。
- 具体示例:
- 社交网络分析:在社交网络中查找用户之间的最短连接。
- 路径规划:如地图中的最短路径规划,帮助导航。
总结对比
在实际问题中,根据具体需求选择最合适的算法:如果需求是查找最短路径,尤其是在无权图中,选择 BFS。如果需要探索所有可能的路径或解决递归问题,使用 DFS。选择合适的遍历方法能提高解决问题的效率和有效性。
假设在一个社交网络中,我们想要找到从用户 A 出发能到达的所有用户,并且希望探索社交网络的至少一层。
- 输入:用户 A 的 ID, 一个社交网络图。
- 目标:获取从用户 A 出发的所有直接联系人和关系。
我们可以针对这个问题分别使用 DFS 和 BFS。
使用 DFS
输出将是:
使用 BFS
输出将是:
通过深度优先搜索(DFS)和广度优先搜索(BFS)两种图遍历方法,我们能够有效地解决多种图论问题。根据不同需求选择正确的遍历方式,当需要寻找图中的所有路径或连通分量时,或处理树结构上的递归问题时,DFS 是一个不错的选择。而当需要寻找最短路径或进行层次遍历时,BFS 是更好的选择。
在实际应用中,评估图的特性和需求,从而选择最合适的遍历方法是极其重要的。此外,应合理管理内存使用,避免栈溢出和内存消耗过高等问题。
PS:感谢每一位志同道合者的阅读,欢迎关注、点赞、评论!
- 上一篇:图论:配对问题与匈牙利算法
- 专栏:「数智通识」
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/15416.html
