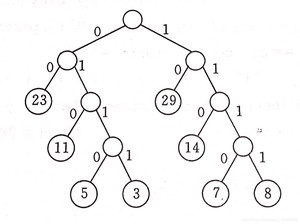
哈夫曼树,又称最优树,时一类带权路径长度最短的树。
从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径,路径上的分支数目称做路径长度。
树的路径长度是从树根到每一结点的路径长度之和。
树的带权路径长度为树中所有叶子结点的带权路径长度之和,通常记作 WPL = ω1l1 + …… + ωnln
假设有 n 个权值{ ω1,ω2,……,ωn },试构造一棵有 n 个叶子结点的二叉树,每个叶子结点带权为 ωi,则其中带权路径长度 WPL 最小的二叉树称做最优二叉树或哈夫曼树。
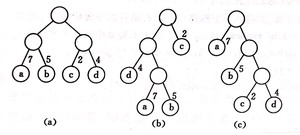
(a)WPL = 7×2+5×2+2×2+4×2=36;
(b)WPL = 7×3+5×3+2×1+4×2=46;
(c)WPL = 7×1+5×2+2×3+4×3=35;
其中(c)树最小。可以验证它恰好为哈夫曼树,即其带权路径长度在所有带权为7、5、2、4的 4 个叶子结点的二叉树中居最小。
- WPL最小
- 给定权值的哈夫曼树可能不只一棵
- 只有度为 2,度为 0 的结点—正则的(严格的)二叉树
- 一棵有 n 个叶子结点的哈夫曼树共有 2n-1 个结点
- 权值越大的叶结点越靠近根结点,而权值越小的叶结点越远离根结点
- 根据给定的 n 个权值 {ω1,ω2,……,ωn} 构成 n 棵二叉树的集合 F={T1,T2,……,Tn},其中每棵二叉树 Ti 中只有一个带权为 ωi 的根结点,其左右子树均空。
- 在 F 中选取两棵根结点的权值最小的树作为左右子树构造一棵新的二叉树,且置新的二叉树的根结点的权值为其左、右子树上根结点的权值之和。
- 在 F 中删除这两棵树,同时将新得到的二叉树加入 F 中。
- 重复 1 和 2,直到 F 只含一棵树为止。这棵树便是哈夫曼树。
若采用相同长度的不同码字代表相应的符号,就称为等长编码。
若要设计长短不等的编码,则必须是任一个字符的编码都不是另一个字符的编码的前缀,这种编码称做前缀编码。
可以利用二叉树来设计二进制的前缀编码。约定左分支表示字符‘0’,右分支表示字符‘1’(左0右1),则可以从根结点到叶子结点的路径上分支字符组成的字符串作为该叶子结点字符的编码。如此得到必为二进制前缀编码,二进制前缀编码也被称为哈夫曼编码。
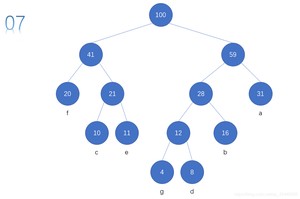
假设用于通信的电文由字符集{a,b,c,d,e,f,g}中的字母构成。它们在电文中出现的频度分别为 {0.31,0.16,0.10,0.08,0.11,0.20,0.04}
为这7个字母设计哈夫曼编码
为这7个字母设计等长编码,至少需要几位二进制数?
哈夫曼编码比等长编码使电文总长压缩多少?
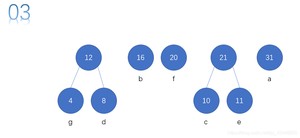
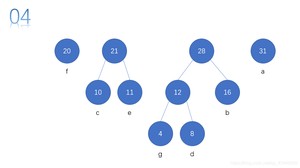
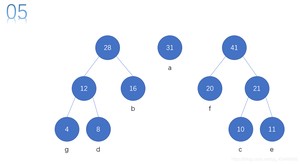
先对权值进行排序。
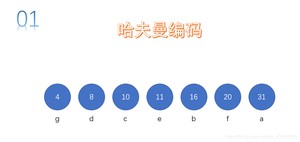
每次从序列中取出两个结点。然后构成一个结点,重新放回序列。
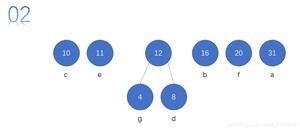
然后再次重复操作,直至,队列剩余一个结点为止。
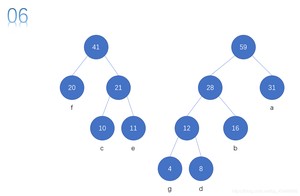
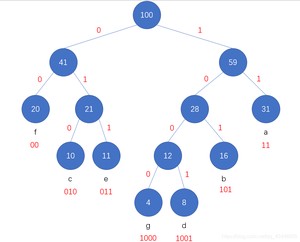
等长编码位数相同表示 7 种符号至少需要 3 位二进制位。
23 =8,所以需要三位二进制数
等长二进制三位共100个字符,占用100 * 3 = 300
哈夫曼编码:2 * 20+ 3 * 10+11* 3+4 * 4+8 * 4+16 * 3+ 31 * 2 = 261
压缩:(300 - 261)/ 300 = 0.13
已知某系统在通信联络中只可能出现 8 种字符,其概率分别为0.05,0.29,0.07,0.08,0.14,0.23,0.03,3.11,试设计哈夫曼编码。
- 码字不同。 哈夫曼所构造的码字不是唯一的,对于同一信息源,无论上述的顺序如何排序,它的平均码长是不会改变,所以他的优点是编码效率唯一性。而二进制编码所构成的码字是唯一。
- 长度不同。 哈夫曼树是依据字符出现概率来构造异字头的平均长度最短的码字,比较精准,二进制编码用预计规定的方法将文字、数字或其他对象编成二进制的数码,或将信息、数据转换成二进制电脉冲信号。二进制是最基础的编码。
- 稳定性不同。 哈夫曼编码的稳定性。如果改变其中一位数据就会产生改变。二进制编码具有抗干扰能力强,可靠性高等优点。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/2448.html