余弦相似度通过测量两个向量的夹角的余弦值来度量它们之间的相似性。0度角的余弦值是1，而其他任何角度的余弦值都不大于1；并且其最小值是-1。从而两个向量之间的角度的余弦值确定两个向量是否大致指向相同的方向。两个向量有相同的指向时，余弦相似度的值为1；两个向量夹角为90°时，余弦相似度的值为0；两个向量指向完全相反的方向时，余弦相似度的值为-1。这结果是与向量的长度无关的，仅仅与向量的指向方向相关。余弦相似度通常用于正空间，因此给出的值为0到1之间。
注意这上下界对任何维度的向量空间中都适用，而且余弦相似性最常用于高维正空间。例如在信息检索中，每个词项被赋予不同的维度，而一个维度由一个向量表示，其各个维度上的值对应于该词项在文档中出现的频率。余弦相似度因此可以给出两篇文档在其主题方面的相似度。
另外，它通常用于文本挖掘中的文件比较。此外，在数据挖掘领域中，会用到它来度量集群内部的凝聚力。
两个向量间的余弦值可以通过使用欧几里得点积公式求出：
给定两个属性向量，A和B，其余弦相似性θ由点积和向量长度给出，如下所示：
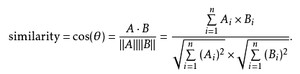
这里的Ai、Bi分别代表向量A和B的各分量。
如果对于上述的公式不是很理解，那就请看这里的公式推导：
（由于不会键盘敲数轴和公式，就直接上笔了）
看一个案例来加深理解：
某购物网站有如下数据：小明购买了T恤a、T恤b、T恤e，小红购买了T恤b、T恤c、小强购买了T恤a、T恤e。
把以上信息转为向量图，代入上述的公式来计算得出相似度，过程如下：
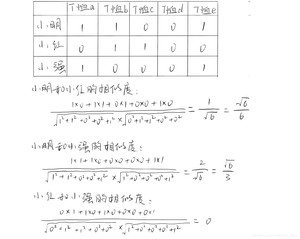由上述的结果便可得到如下结论：小明和小红这两个用户有一定的相似度，但是不大，因为他们只有一个共同商品；小明和小强这两个用户相似度最大，因为他们有两个共同商品；而小红和小强的相似度为0，因为小红买的T恤小强都没有买。
转自：https://blog.csdn.net/smile_shujie/article/details/
版权声明：
本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。
本文网址：https://www.mushiming.com/mjsbk/2758.html