二叉排序树是动态查找表的一种,也是常用的表示方法。
其中,它具有如下性质:
1.若它的左子树非空,则其左子树的所有节点的关键值都小于根节点的关键值。
2.若它的右子树非空,则其右子树的所有节点的关键值都大于根结点的关键值。
3.它的左右子树也分别都是二叉排序树。
PS:对二叉排序树进行中序遍历,得到的序列,总会是一个升序的数列。
我们使用C语言来建立。
对于删除二叉排序树的节点,我们有必要花大功夫来讨论一下。
对于删除二叉排序树的某个节点,大致有以下四种情况:
假设我们要删除的节点指定为P。
此时删除P节点,只需要P节点的父节点的左/右子树赋值NULL,并且free掉P节点即可。
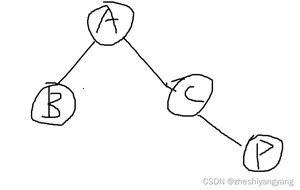
值得注意的是,还有一种特殊情况,那就是P节点本身就是根节点,也就是这个树只有P节点一个
节点。
那么此时,我们只需要返回NULL,并且free掉P节点即可。

在这种情况下,我们注意到P的右子树不是空的,如下图所示:
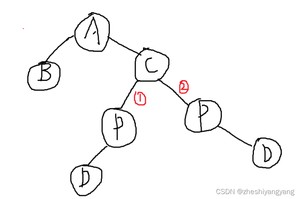
此时我们只需要令P节点的父节点C的右子树/左子树为P的右子树即可。
不过值得注意的是,此时仍有可能P是根节点,此时我们需要令根节点 = p的右子树,并且free掉p
节点即可。
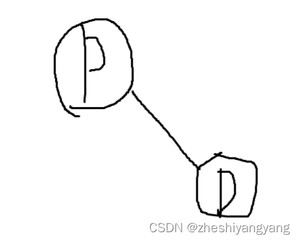
此时我们注意到,这种情况根情况2(P节点的左子树为空)非常相似。
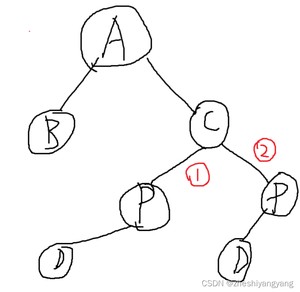
此时我们只需要令P的父节点C的左/右子树等于P的左子树即可。
不过此时P节点仍有可能作为根节点出现,此时我们只需要令根节点等于P的左子树即可。
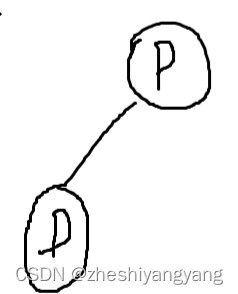
这种情况无疑是最复杂的一种情况,因为此时我们要牵扯一个大小的排序。
因此,我们可以令P节点的Key值等于P节点的直接前驱(直接后驱)的Key值,之后删掉直接前驱(直
接后驱)即可。
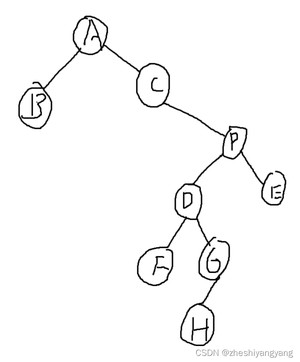
注意到此时的P节点的直接前驱是G(即P节点的左子树的最右侧的一个节点)。
那么此时我们可以令P节点的Key值等于G节点的Key值,同时free掉G节点即可完成操作。
不过,比较重要的一点是,G节点的左子树不一定为空,此时我们仍需要让G节点的父节点的右子
树等于G节点的左子树。
注意到,当P节点作为根结点的时候并不会出现特殊的情况,但是当P节点的前驱节点就是P的左子
树,我们需要另外的讨论,如下图所示:
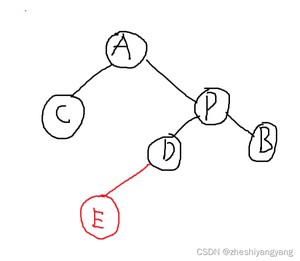
注意到此时P的直接前驱节点就是D,但是如果我们直接删除D,那么D的左子树此时应该给P的左
子树。
注意到P也是D的一个父节点,P同时还是D的一个直接后继节点,此时就是一种特殊情况,需要让
P的左子树等于D的左子树,而不是D的父节点的右子树等于D的左子树!!!
代码实现:
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/3096.html
