这篇文章将会详细透彻地讲清楚 Java 的 HashMap,包括 hash 方法的原理、HashMap 的扩容机制、HashMap 的加载因子为什么是 0.75 而不是 0.6、0.8,以及 HashMap 为什么是线程不安全的,基本上 HashMap 的常见面试题,都会在这一篇文章里讲明白。
HashMap 是 Java 中常用的数据结构之一,用于存储键值对。在 HashMap 中,每个键都映射到一个唯一的值,可以通过键来快速访问对应的值,算法时间复杂度可以达到 O(1)。
HashMap 不仅在日常开发中经常用到,在面试中也是重点考察的对象。
以下是 HashMap 增删改查的简单例子:
1)增加元素:
将一个键值对(元素)添加到 HashMap 中,可以使用 put() 方法。例如,将名字和年龄作为键值对添加到 HashMap 中:
2)删除元素:
从 HashMap 中删除一个键值对,可以使用 remove() 方法。例如,删除名字为 "沉默" 的键值对:
3)修改元素:
修改 HashMap 中的一个键值对,可以使用 put() 方法。例如,将名字为 "沉默" 的年龄修改为 30:
为什么和添加元素的方法一样呢?这个我们后面会讲,先简单说一下,是因为 HashMap 的键是唯一的,所以再次 put 的时候会覆盖掉之前的键值对。
4)查找元素:
从 HashMap 中查找一个键对应的值,可以使用 get() 方法。例如,查找名字为 "沉默" 的年龄:
在实际应用中,HashMap 可以用于缓存、索引等场景。例如,可以将用户 ID 作为键,用户信息作为值,将用户信息缓存到 HashMap 中,以便快速查找。又如,可以将关键字作为键,文档 ID 列表作为值,将文档索引缓存到 HashMap 中,以便快速搜索文档。
HashMap 的实现原理是基于哈希表的,它的底层是一个数组,数组的每个位置可能是一个链表或红黑树,也可能只是一个键值对(后面会讲)。当添加一个键值对时,HashMap 会根据键的哈希值计算出该键对应的数组下标(索引),然后将键值对插入到对应的位置。
当通过键查找值时,HashMap 也会根据键的哈希值计算出数组下标,并查找对应的值。
简单了解 HashMap 后,我们来讨论第一个问题:hash 方法的原理,对吃透 HashMap 会大有帮助。
来看一下 hash 方法的源码(JDK 8 中的 HashMap):
这段代码究竟是用来干嘛的呢?
将 key 的 hashCode 值进行处理,得到最终的哈希值。
怎么理解这句话呢?不要着急。
我们来 new 一个 HashMap,并通过 put 方法添加一个元素。
来看一下 put 方法的源码。
看到 hash 方法的身影了吧?
前面也说了,HashMap 的底层是通过数组的形式实现的,初始大小是 16(这个后面会讲),先记住。
也就是说,HashMap 在添加第一个元素的时候,需要通过键的哈希码在大小为 16 的数组中确定一个位置(索引),怎么确定呢?
为了方便大家直观的感受,我这里画了一副图,16 个方格子(可以把它想象成一个一个桶),每个格子都有一个编号,对应大小为 16 的数组下标(索引)。
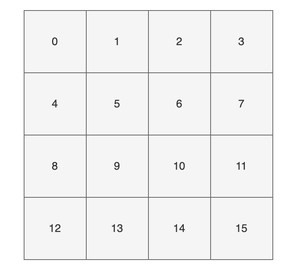
现在,我们要把 key 为 “chenmo”,value 为“沉默”的键值对放到这 16 个格子中的一个。
怎么确定位置(索引)呢?
我先告诉大家结论,通过这个与运算 ,其中变量 n 为数组的长度,变量 hash 就是通过 方法计算后的结果。
那“chenmo”这个 key 计算后的位置(索引)是多少呢?
答案是 8,也就是说 会把 key 为 “chenmo”,value 为“沉默”的键值对放到下标为 8 的位置上(也就是索引为 8 的桶上)。
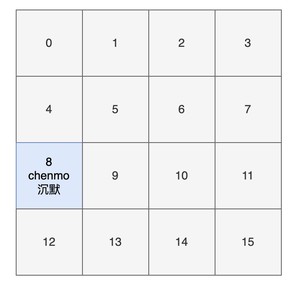
这样大家就会对 HashMap 存放键值对(元素)的时候有一个大致的印象。其中的一点是,hash 方法对计算键值对的位置起到了至关重要的作用。
回到 hash 方法:
下面是对该方法的一些解释:
- 参数 key:需要计算哈希码的键值。
- :这是一个三目运算符,如果键值为 null,则哈希码为 0(依旧是说如果键为 null,则存放在第一个位置);否则,通过调用方法获取键的哈希码,并将其与右移 16 位的哈希码进行异或运算。
- 运算符:异或运算符是 Java 中的一种位运算符,它用于将两个数的二进制位进行比较,如果相同则为 0,不同则为 1。
- :将哈希码向右移动 16 位,相当于将原来的哈希码分成了两个 16 位的部分。
- 最终返回的是经过异或运算后得到的哈希码值。
这短短的一行代码,汇聚不少计算机巨佬们的聪明才智。
理论上,哈希值(哈希码)是一个 int 类型,范围从- 到 。
前后加起来大概 40 亿的映射空间,只要哈希值映射得比较均匀松散,一般是不会出现哈希碰撞(哈希冲突会降低 HashMap 的效率)。
但问题是一个 40 亿长度的数组,内存是放不下的。HashMap 扩容之前的数组初始大小只有 16,所以这个哈希值是不能直接拿来用的,用之前要和数组的长度做与运算(前文提到的 ,有些地方叫取模预算,有些地方叫取余运算),用得到的值来访问数组下标才行。
那这里就顺带补充一些取模预算/取余运算和与运算的知识点哈。
取模运算(Modulo Operation)和取余运算(Remainder Operation)从严格意义上来讲,是两种不同的运算方式,它们在计算机中的实现也不同。
在 Java 中,通常使用 % 运算符来表示取余,用 来表示取模。
- 当操作数都是正数的话,取模运算和取余运算的结果是一样的。
- 只有当操作数出现负数的情况,结果才会有所不同。
- 取模运算的商向负无穷靠近;取余运算的商向 0 靠近。这是导致它们两个在处理有负数情况下,结果不同的根本原因。
- 当数组的长度是 2 的 n 次方,或者 n 次幂,或者 n 的整数倍时,取模运算/取余运算可以用位运算来代替,效率更高,毕竟计算机本身只认二进制嘛。
我们通过一个实际的例子来看一下。
输出结果如下所示:
为什么会有这样的结果呢?
首先,我们来考虑一下常规除法。当我们将一个数除以另一个数时,我们将得到一个商和一个余数。
例如,当我们把 7 除以 3 时,我们得到商 2 和余数 1,因为 (7 = 3 × 2 + 1)。
推荐阅读:Java 取模和取余
01、取余:
余数的定义是基于常规除法的,所以它的符号总是与被除数相同。商趋向于 0。
例如,对于 ,余数是 。因为 -7 / 3 可以有两种结果,一种是商 -2 余 -1;一种是商 -3 余 2,对吧?
因为取余的商趋向于 0,-2 比 -3 更接近于 0,所以取余的结果是 -1。
02、取模:
取模也是基于除法的,只不过它的符号总是与除数相同。商趋向于负无穷。
例如,对于 ,结果是 。同理,因为 -7 / 3 可以有两种结果,一种是商 -2 余 -1;一种是商 -3 余 2,对吧?
因为取模的商趋向于负无穷,-3 比 -2 更接近于负无穷,所以取模的结果是 2。
需要注意的是,不管是取模还是取余,除数都不能为 0,因为取模和取余都是基于除法运算的。
03、与运算:
当除数和被除数都是正数的情况下,取模运算和取余运算的结果是一样的。
比如说,7 对 3 取余,和 7 对 3 取模,结果都是 1。因为两者都是基于除法运算的,7 / 3 的商是 2,余数是 1。
于是,我们会在很多地方看到,取余就是取模,取模就是取余。这是一种不准确的说法,基于操作数都是正数的情况下。
对于 HashMap 来说,它需要通过 来确定元素在数组中的位置,这种做法可以在很大程度上让元素均匀的分布在数组中。
比如说,数组长度是 3,hash 是 7,那么 7 % 3 的结果就是 1,也就是此时可以把元素放在下标为 1 的位置。
当 hash 是 8,8 % 3 的结果就是 2,也就是可以把元素放在下标为 2 的位置。
当 hash 是 9,9 % 3 的结果就是 0,也就是可以把元素放在下标为 0 的位置上。
是不是很奇妙,数组的大小为 3,刚好 3 个位置都利用上了。
那为什么 HashMap 在计算下标的时候,并没有直接使用取余运算(或者取模运算),而是直接使用位与运算 & 呢?
因为当数组的长度是 2 的 n 次方时,。
比如说 9 % 4 = 1,9 的二进制是 1001,4 - 1 = 3,3 的二进制是 0011,9 & 3 = 1001 & 0011 = 0001 = 1。
再比如说 10 % 4 = 2,10 的二进制是 1010,4 - 1 = 3,3 的二进制是 0011,10 & 3 = 1010 & 0011 = 0010 = 2。
当数组的长度不是 2 的 n 次方时, 和 的结果就不一致了。
比如说 7 % 3 = 1,7 的二进制是 0111,3 - 1 = 2,2 的二进制是 0010,7 & 2 = 0111 & 0010 = 0010 = 2。
那为什么呢?
因为从二进制角度来看,hash / length = hash / ${2^n}$ = hash >> n,即把 hash 右移 n 位,此时得到了 hash / ${2^n}$ 的商。
而被移调的部分,则是 hash % ${2^n}$,也就是余数。
${2^n}$ 的二进制形式为 1,后面跟着 n 个 0,那 ${2^n}$ - 1 的二进制则是 n 个 1。例如 8 = ${2^3}$,二进制是 1000,7 = ${2^3}$ - 1,二进制为 0111。
的操作是求 hash 除以 ${2^n}$ 的余数。在二进制中,这个操作的结果就是 hash 的二进制表示中最低 n 位的值。
因为在 ${2^n}$ 取模的操作中,高于 ${2^n}$ 表示位的所有数值对结果没有贡献,只有低于这个阈值的部分才决定余数。
比如说 26 的二进制是 11010,要计算 26 % 8,8 是 ${2^3}$,所以我们关注的是 26 的二进制表示中最低 3 位:11010 的最低 3 位是 010。
010 对应于十进制中的 2,26 % 8 的结果是 2。
当执行时,实际上是保留 hash 二进制表示的最低 n 位,其他高位都被清零。
& 与运算:两个操作数中位都为 1,结果才为 1,否则结果为 0。
举个例子,hash 为 14,n 为 3,也就是数组长度为 ${2^3}$,也就是 8。
保留 14 的最低 3 位,高位被清零。
从此,两个运算 和 有了完美的闭环。在计算机中,位运算的速度要远高于取余运算,因为计算机本质上就是二进制嘛。
HashMap 的取模运算有两处。
一处是往 HashMap 中 put 的时候(会调用私有的 方法):
其中 为取模运算,为什么没用 ,我们随后解释。
一处是从 HashMap 中 get 的时候(会调用 方法):
看到没,取模运算 再次出现,说简单点,就是把键的哈希码经过 方法计算后,再和(数组长度-1)做了一个“与”运算。
可能大家在疑惑:取模运算难道不该用 吗?为什么要用位运算 呢?
这是因为 运算比 更加高效,并且当 b 为 2 的 n 次方时,存在下面这样一个公式。
a % b = a & (b-1)
用 ${2^n}$ 替换下 b 就是:
a % ${2^n}$ = a & (${2^n}$-1)
我们来验证一下,假如 a = 14,b = 8,也就是 ${2^3}$,n=3。
14%8(余数为 6)。
14 的二进制为 1110,8 的二进制 1000,8-1 = 7,7 的二进制为 0111,1110&0111=0110,也就是 0${20}$+1`*`${21}$+1${22}$+0`*`${23}$=0+2+4+0=6,14%8 刚好也等于 6。
害,计算机就是这么讲道理,没办法,😝
这也正好解释了为什么 HashMap 的数组长度要取 2 的整次方。
为什么会这样巧呢?
因为(数组长度-1)正好相当于一个“低位掩码”——这个掩码的低位最好全是 1,这样 & 操作才有意义,否则结果就肯定是 0。
a&b 操作的结果是:a、b 中对应位同时为 1,则对应结果位为 1,否则为 0。例如 5&3=1,5 的二进制是 0101,3 的二进制是 0011,5&3=0001=1。
2 的整次幂刚好是偶数,偶数-1 是奇数,奇数的二进制最后一位是 1,保证了 的最后一位可能为 0,也可能为 1(取决于 hash 的值),即 & 运算后的结果可能为偶数,也可能为奇数,这样便可以保证哈希值的均匀分布。
换句话说,& 操作的结果就是将哈希值的高位全部归零,只保留低位值。
假设某哈希值的二进制为 ,用它来做 & 运算,我们来看一下结果。
我们知道,HashMap 的初始长度为 16,16-1=15,二进制是 (高位用 0 来补齐):
因为 15 的高位全部是 0,所以 & 运算后的高位结果肯定也是 0,只剩下 4 个低位 ,也就是十进制的 5。
这样,哈希值为 的键就会放在数组的第 5 个位置上。
当然了,如果你是新手,上面这些 01 串看不太懂,也没关系。记住 &运算是为了计算数组的下标就可以了。
- put 的时候计算下标,把键值对放到对应的桶上。
- get 的时候通过下标,把键值对从对应的桶上取出来。
看下面这个图。
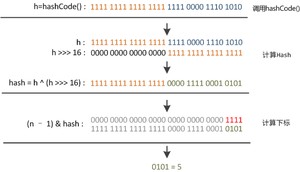
某哈希值为 ,将它右移 16 位(h >>> 16),刚好是 ,再进行异或操作(h ^ (h >>> 16)),结果是
异或()运算是基于二进制的位运算,采用符号 XOR 或者来表示,运算规则是:如果是同值取 0、异值取 1
由于混合了原来哈希值的高位和低位,所以低位的随机性加大了(掺杂了部分高位的特征,高位的信息也得到了保留)。
结果再与数组长度-1()做取模运算,得到的下标就是 ,也就是 5。
还记得之前我们假设的某哈希值 吗?在没有调用 hash 方法之前,与 15 做取模运算后的结果也是 5,我们不妨来看看调用 hash 之后的取模运算结果是多少。
某哈希值 (补齐 32 位),将它右移 16 位(h >>> 16),刚好是 ,再进行异或操作(h ^ (h >>> 16)),结果是
结果再与数组长度-1()做取模运算,得到的下标就是 ,也就是 0。
综上所述,hash 方法是用来做哈希值优化的,把哈希值右移 16 位,也就正好是自己长度的一半,之后与原哈希值做异或运算,这样就混合了原哈希值中的高位和低位,增大了随机性。
说白了,hash 方法就是为了增加随机性,让数据元素更加均衡的分布,减少碰撞。
我这里写了一段测试代码,假如 HashMap 的容量就是第一次扩容时候的 16,我在里面放了五个键值对,来看一下键的 hash 值(经过 方法计算后的哈希码)和索引(取模运算后)
输出结果如下所示:
也就是说,此时还没有发生哈希冲突,索引值都是比较均匀分布的,5、6、8、9、11,这其中的很大一部分功劳,就来自于 hash 方法。
hash 方法的主要作用是将 key 的 hashCode 值进行处理,得到最终的哈希值。由于 key 的 hashCode 值是不确定的,可能会出现哈希冲突,因此需要将哈希值通过一定的算法映射到 HashMap 的实际存储位置上。
hash 方法的原理是,先获取 key 对象的 hashCode 值,然后将其高位与低位进行异或操作,得到一个新的哈希值。为什么要进行异或操作呢?因为对于 hashCode 的高位和低位,它们的分布是比较均匀的,如果只是简单地将它们加起来或者进行位运算,容易出现哈希冲突,而异或操作可以避免这个问题。
然后将新的哈希值取模(mod),得到一个实际的存储位置。这个取模操作的目的是将哈希值映射到桶(Bucket)的索引上,桶是 HashMap 中的一个数组,每个桶中会存储着一个链表(或者红黑树),装载哈希值相同的键值对(没有相同哈希值的话就只存储一个键值对)。
总的来说,HashMap 的 hash 方法就是将 key 对象的 hashCode 值进行处理,得到最终的哈希值,并通过一定的算法映射到实际的存储位置上。这个过程决定了 HashMap 内部键值对的查找效率。
好,理解了 hash 方法后我们来看第二个问题,HashMap 的扩容机制。
大家都知道,数组一旦初始化后大小就无法改变了,所以就有了 ArrayList这种“动态数组”,可以自动扩容。
HashMap 的底层用的也是数组。向 HashMap 里不停地添加元素,当数组无法装载更多元素时,就需要对数组进行扩容,以便装入更多的元素;除此之外,容量的提升也会相应地提高查询效率,因为“桶(坑)”更多了嘛,原来需要通过链表存储的(查询的时候需要遍历),扩容后可能就有自己专属的“坑位”了(直接就能查出来)。
来看这个例子,容量我们定位 16:
来看输出结果:
看到没?
- fangxiaowan(方小婉)和 yaoxiaojuan(姚小娟)的索引都是 6;
- chenqingyang(陈清扬)和 yexin(叶辛)的索引都是 9
这就意味着,要采用拉链法(后面会讲)将他们放在同一个索引的链表上。查询的时候,就不能直接通过索引的方式直接拿到(时间复杂度为 O(1)),而要通过遍历的方式(时间复杂度为 O(n))。
那假如把数组的长度由 16 扩容为 32 呢?
将之前示例中的 n 由 16 改为 32 即可得到如下的答案:
可以看到:
- 虽然 chenqingyang(陈清扬)和 yexin(叶辛)的索引仍然是 9。
- 但 fangxiaowan(方小婉)的索引为 6,yaoxiaojuan(姚小娟)的索引由 6 变为 22,各自都有坑了。
当然了,数组是无法自动扩容的,所以如果要扩容的话,就需要新建一个大的数组,然后把之前小的数组的元素复制过去,并且要重新计算哈希值和重新分配桶(重新散列),这个过程也是挺耗时的。
HashMap 的扩容是通过 resize 方法来实现的,JDK 8 中融入了红黑树(链表长度超过 8 的时候,会将链表转化为红黑树来提高查询效率),对于新手来说,可能比较难理解。
为了减轻大家的学习压力,就还使用 JDK 7 的源码,搞清楚了 JDK 7 的,再看 JDK 8 的就会轻松很多。
来看 Java7 的 resize 方法源码,我加了注释:
该方法接收一个新的容量 newCapacity,然后将 HashMap 的容量扩大到 newCapacity。
首先,方法获取当前 HashMap 的旧数组 oldTable 和旧容量 oldCapacity。如果旧容量已经达到 HashMap 支持的最大容量 MAXIMUM_CAPACITY( 2 的 30 次方),就将新的阈值 threshold 调整为 Integer.MAX_VALUE(2 的 31 次方 - 1),这是因为 HashMap 的容量不能超过 MAXIMUM_CAPACITY。
因为 2,147,483,647(Integer.MAX_VALUE) - 1,073,741,824(MAXIMUM_CAPACITY) = 1,073,741,823,刚好相差一倍(HashMap 每次扩容都是之前的一倍)。
接着,方法创建一个新的数组 newTable,并将旧数组 oldTable 中的元素转移到新数组 newTable 中。转移过程是通过调用 transfer 方法来实现的。该方法遍历旧数组中的每个桶,并将每个桶中的键值对重新计算哈希值后,将其插入到新数组对应的桶中。
转移完成后,方法将 HashMap 内部的数组引用 table 指向新数组 newTable,并重新计算阈值 threshold。新的阈值是新容量 newCapacity 乘以负载因子 loadFactor 的结果,但如果计算结果超过了 HashMap 支持的最大容量 MAXIMUM_CAPACITY,则将阈值设置为 MAXIMUM_CAPACITY + 1,这是因为 HashMap 的元素数量不能超过 MAXIMUM_CAPACITY。
那 newCapacity 是如何计算的呢?
新容量 newCapacity 被初始化为原容量 oldCapacity 的两倍。然后,如果 newCapacity 超过了 HashMap 的容量限制 MAXIMUM_CAPACITY(2^30),就将 newCapacity 设置为 MAXIMUM_CAPACITY。如果 newCapacity 小于默认初始容量 DEFAULT_INITIAL_CAPACITY(16),就将 newCapacity 设置为 DEFAULT_INITIAL_CAPACITY。这样可以避免新容量太小或太大导致哈希冲突过多或者浪费空间。
Java 8 的时候,newCapacity 的计算方式发生了一些细微的变化。
注意, 变成了 ,出现了左移(),这里简单介绍一下:
十进制 39 用 8 位的二进制来表示,就是 00,左移两位后是 (低位用 0 补上),再转成十进制数就是 156。
移位运算通常可以用来代替乘法运算和除法运算。例如,将 0010011(39)左移两位就是 (156),刚好变成了原来的 4 倍。
实际上呢,二进制数左移后会变成原来的 2 倍、4 倍、8 倍,记住这个就好。
接下来,来说 transfer 方法,该方法用来转移,将旧的小数组元素拷贝到新的大数组中。
该方法接受一个新的 Entry 数组 newTable 和一个布尔值 rehash 作为参数,其中 newTable 表示新的哈希表,rehash 表示是否需要重新计算键的哈希值。
在方法中,首先获取新哈希表(数组)的长度 newCapacity,然后遍历旧哈希表中的每个 Entry。对于每个 Entry,使用拉链法将相同 key 值的不同 value 值存储在同一个链表中。如果 rehash 为 true,则需要重新计算键的哈希值,并将新的哈希值存储在 Entry 的 hash 属性中。
接着,根据新哈希表的长度和键的哈希值,计算 Entry 在新数组中的位置 i,然后将该 Entry 添加到新数组的 i 位置上。由于新元素需要被放在链表的头部,因此将新元素的下一个元素设置为当前数组位置上的元素。
最后,遍历完旧哈希表中的所有元素后,转移工作完成,新的哈希表 newTable 已经包含了旧哈希表中的所有元素。
注意,,也就是使用了单链表的头插入方式,同一位置上新元素总会被放在链表的头部位置;这样先放在一个索引上的元素最终会被放到链表的尾部,这就会导致在旧数组中同一个链表上的元素,通过重新计算索引位置后,有可能被放到了新数组的不同位置上。
为了解决这个问题,Java 8 做了很大的优化(讲扩容的时候会讲到)。
JDK 8 的扩容源代码:
1、获取原来的数组 table、数组长度 oldCap 和阈值 oldThr。
2、如果原来的数组 table 不为空,则根据扩容规则计算新数组长度 newCap 和新阈值 newThr,然后将原数组中的元素复制到新数组中。
3、如果原来的数组 table 为空但阈值 oldThr 不为零,则说明是通过带参数构造方法创建的 HashMap,此时将阈值作为新数组长度 newCap。
4、如果原来的数组 table 和阈值 oldThr 都为零,则说明是通过无参数构造方法创建的 HashMap,此时将默认初始容量 和默认负载因子 计算出新数组长度 newCap 和新阈值 newThr。
5、计算新阈值 threshold,并将其赋值给成员变量 threshold。
6、创建新数组 newTab,并将其赋值给成员变量 table。
7、如果旧数组 oldTab 不为空,则遍历旧数组的每个元素,将其复制到新数组中。
8、返回新数组 newTab。
在 JDK 7 中,定位元素位置的代码是这样的:
其实就相当于用键的哈希值和数组大小取模,也就是 。
那我们来假设:
- 数组 table 的长度为 2
- 键的哈希值为 3、7、5
取模运算后,键发生了哈希冲突,都到 上了。那么扩容前就是这个样子。
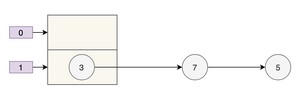
数组的容量为 2,key 为 3、7、5 的元素在 上,需要通过拉链法来解决哈希冲突。
假设负载因子 loadFactor 为 1,也就是当元素的个数大于 table 的长度时进行扩容。
扩容后的数组容量为 4。
- key 3 取模(3%4)后是 3,放在 上。
- key 7 取模(7%4)后是 3,放在 上的链表头部。
- key 5 取模(5%4)后是 1,放在 上。
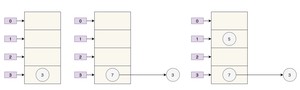
7 跑到 3 的前面了,因为 JDK 7 使用的是头插法。
同时,扩容后的 5 跑到了下标为 1 的位置。
最好的情况就是,扩容后的 7 在 3 的后面,5 在 7 的后面,保持原来的顺序。
JDK 8 完全扭转了这个局面,因为 JDK 8 的哈希算法进行了优化,当数组长度为 2 的幂次方时,能够很巧妙地解决 JDK 7 中遇到的问题。
JDK 8 的扩容代码如下所示:
新索引的计算方式是 ,和 JDK 7 的 没什么大的差别,差别主要在 hash 方法上,JDK 8 是这样:
过将键的返回的 32 位哈希值与这个哈希值无符号右移 16 位的结果进行异或。
JDK 7 是这样:
我们用 JDK 8 的哈希算法来计算一下哈希值,就会发现别有洞天。
假设扩容前的数组长度为 16(n-1 也就是二进制的 0000 1111,1X$20$+1X$21$+1X$22$+1X$23$=1+2+4+8=15),key1 为 5(二进制为 0000 0101),key2 为 21(二进制为 0001 0101)。
- key1 和 n-1 做 & 运算后为 0000 0101,也就是 5;
- key2 和 n-1 做 & 运算后为 0000 0101,也就是 5。
- 此时哈希冲突了,用拉链法来解决哈希冲突。
现在,HashMap 进行了扩容,容量为原来的 2 倍,也就是 32(n-1 也就是二进制的 0001 1111,1X$20$+1X$21$+1X$22$+1X$23$+1X$2^4$=1+2+4+8+16=31)。
- key1 和 n-1 做 & 运算后为 0000 0101,也就是 5;
- key2 和 n-1 做 & 运算后为 0001 0101,也就是 21=5+16,也就是数组扩容前的位置+原数组的长度。
神奇吧?

也就是说,在 JDK 8 的新 hash 算法下,数组扩容后的索引位置,要么就是原来的索引位置,要么就是“原索引+原来的容量”,遵循一定的规律。
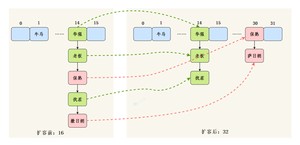
当然了,这个功劳既属于新的哈希算法,也离不开 n 为 2 的整数次幂这个前提,这是它俩通力合作后的结果 。
当我们往 HashMap 中不断添加元素时,HashMap 会自动进行扩容操作(条件是元素数量达到负载因子(load factor)乘以数组长度时),以保证其存储的元素数量不会超出其容量限制。
在进行扩容操作时,HashMap 会先将数组的长度扩大一倍,然后将原来的元素重新散列到新的数组中。
由于元素的位置是通过 key 的 hash 和数组长度进行与运算得到的,因此在数组长度扩大后,元素的位置也会发生一些改变。一部分索引不变,另一部分索引为“原索引+旧容量”。
上一个问题提到了加载因子(或者叫负载因子),那么这个问题我们来讨论为什么加载因子是 0.75 而不是 0.6、0.8。
我们知道,HashMap 是用数组+链表/红黑树实现的,我们要想往 HashMap 中添加数据(元素/键值对)或者取数据,就需要确定数据在数组中的下标(索引)。
先把数据的键进行一次 hash:
再做一次取模运算确定下标:
那这样的过程容易产生两个问题:
- 数组的容量过小,经过哈希计算后的下标,容易出现冲突;
- 数组的容量过大,导致空间利用率不高。
加载因子是用来表示 HashMap 中数据的填满程度:
加载因子 = 填入哈希表中的数据个数 / 哈希表的长度
这就意味着:
- 加载因子越小,填满的数据就越少,哈希冲突的几率就减少了,但浪费了空间,而且还会提高扩容的触发几率;
- 加载因子越大,填满的数据就越多,空间利用率就高,但哈希冲突的几率就变大了。
好难!!!!
这就必须在“哈希冲突”与“空间利用率”两者之间有所取舍,尽量保持平衡,谁也不碍着谁。
我们知道,HashMap 是通过拉链法来解决哈希冲突的。
为了减少哈希冲突发生的概率,当 HashMap 的数组长度达到一个临界值的时候,就会触发扩容,扩容后会将之前小数组中的元素转移到大数组中,这是一个相当耗时的操作。
这个临界值由什么来确定呢?
临界值 = 初始容量 * 加载因子
一开始,HashMap 的容量是 16:
加载因子是 0.75:
也就是说,当 16*0.75=12 时,会触发扩容机制。
为什么加载因子会选择 0.75 呢?为什么不是 0.8、0.6 呢?
这跟统计学里的一个很重要的原理——泊松分布有关。
是时候上维基百科了:
泊松分布,是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松在 1838 年时提出。它会对随机事件的发生次数进行建模,适用于涉及计算在给定的时间段、距离、面积等范围内发生随机事件的次数的应用情形。
阮一峰老师曾在一篇博文中详细的介绍了泊松分布和指数分布,大家可以去看一下。
链接:https://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html
具体是用这么一个公式来表示的。
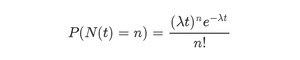
等号的左边,P 表示概率,N 表示某种函数关系,t 表示时间,n 表示数量。
在 HashMap 的 doc 文档里,曾有这么一段描述:
为了便于大家的理解,这里来重温一下 HashMap 的拉链法和红黑树结构。
Java 8 之前,HashMap 使用链表来解决冲突,即当两个或者多个键映射到同一个桶时,它们被放在同一个桶的链表上。当链表上的节点(Node)过多时,链表会变得很长,查找的效率(LinkedList 的查找效率为 O(n))就会受到影响。
Java 8 中,当链表的节点数超过一个阈值(8)时,链表将转为红黑树(节点为 TreeNode),红黑树(在讲TreeMap时会细说)是一种高效的平衡树结构,能够在 O(log n) 的时间内完成插入、删除和查找等操作。这种结构在节点数很多时,可以提高 HashMap 的性能和可伸缩性。
好,有了这个背景,我们来把上面的 doc 文档翻译为中文:
虽然这段话的本意更多的是表示 jdk 8 中为什么拉链长度超过 8 的时候进行了红黑树转换,但提到了 0.75 这个加载因子,但没提到底为什么。
为了搞清楚到底为什么,我看到了这篇文章:
参考链接:https://segmentfault.com/a/08658
里面提到了一个概念:二项分布(Binomial Distribution)。
在做一件事情的时候,其结果的概率只有 2 种情况,和抛硬币一样,不是正面就是反面。
假如,我们做了 N 次实验,那么在每次试验中只有两种可能的结果,并且每次实验是独立的,不同实验之间互不影响,每次实验成功的概率都是一样的。
以此理论为基础:我们往哈希表中扔数据,如果发生哈希冲突就为失败,否则为成功。
我们可以设想,实验的 hash 值是随机的,并且经过 hash 运算的键都会映射到 hash 表的地址空间上,那么这个结果也是随机的。所以,每次 put 的时候就相当于我们在扔一个 16 面(HashMap 第一次扩容后的数组默认长度为 16)的骰子,扔骰子实验那肯定是相互独立的。碰撞发生即扔了 n 次有出现重复数字。
然后,我们的目的是啥呢?
就是掷了 k 次骰子,没有一次是相同的概率,需要尽可能的大些,一般意义上我们肯定要大于 0.5(这个数是个理想数)。
于是,n 次事件里面,碰撞为 0 的概率,由上面公式得:
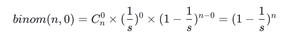
这个概率值需要大于 0.5,我们认为这样的 hashmap 可以提供很低的碰撞率。所以:

这时候,我们对于该公式其实最想求的时候长度 s 的时候,n 为多少次就应该进行扩容了?而负载因子则是$n/s$的值。所以推导如下:

所以可以得到
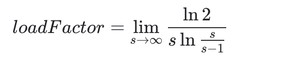
其中
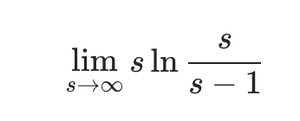
这就是一个求 函数极限问题,这里我们先令$s = m+1(m o infty)$则转化为
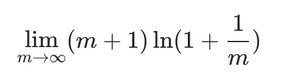
我们再令 $x = frac{1}{m} (x o 0)$ 则有,
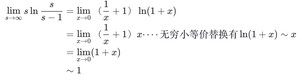
所以
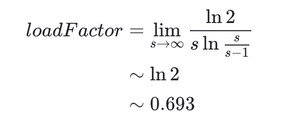
考虑到 HashMap 的容量有一个要求:它必须是 2 的 n 次幂。当加载因子选择了 0.75 就可以保证它与容量的乘积为整数。
除了 0.75,0.5~1 之间还有 0.625(5/8)、0.875(7/8)可选,从中位数的角度,挑 0.75 比较完美。另外,维基百科上说,拉链法(解决哈希冲突的一种)的加载因子最好限制在 0.7-0.8 以下,超过 0.8,查表时的 CPU 缓存不命中(cache missing)会按照指数曲线上升。
综上,0.75 是个比较完美的选择。
HashMap 的加载因子(load factor,直译为加载因子,意译为负载因子)是指哈希表中填充元素的个数与桶的数量的比值,当元素个数达到负载因子与桶的数量的乘积时,就需要进行扩容。这个值一般选择 0.75,是因为这个值可以在时间和空间成本之间做到一个折中,使得哈希表的性能达到较好的表现。
如果负载因子过大,填充因子较多,那么哈希表中的元素就会越来越多地聚集在少数的桶中,这就导致了冲突的增加,这些冲突会导致查找、插入和删除操作的效率下降。同时,这也会导致需要更频繁地进行扩容,进一步降低了性能。
如果负载因子过小,那么桶的数量会很多,虽然可以减少冲突,但是在空间利用上面也会有浪费,因此选择 0.75 是为了取得一个平衡点,即在时间和空间成本之间取得一个比较好的平衡点。
总之,选择 0.75 这个值是为了在时间和空间成本之间达到一个较好的平衡点,既可以保证哈希表的性能表现,又能够充分利用空间。
其实这个问题也不用说太多,但考虑到面试的时候有些面试官会问,那就简单说一下。
三方面原因:
- 多线程下扩容会死循环
- 多线程下 put 会导致元素丢失
- put 和 get 并发时会导致 get 到 null
众所周知,HashMap 是通过拉链法来解决哈希冲突的,也就是当哈希冲突时,会将相同哈希值的键值对通过链表的形式存放起来。
JDK 7 时,采用的是头部插入的方式来存放链表的,也就是下一个冲突的键值对会放在上一个键值对的前面(讲扩容的时候讲过了)。扩容的时候就有可能导致出现环形链表,造成死循环。
resize 方法的源码:
transfer 方法用来转移,将小数组的元素拷贝到新的数组中。
注意 和 这两行代码,就会将同一位置上的新元素被放在链表的头部。
扩容前的样子假如是下面这样子。
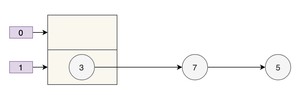
那么正常扩容后就是下面这样子。
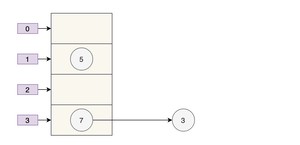
假设现在有两个线程同时进行扩容,线程 A 在执行到 被挂起,此时线程 A 中:e=3、next=7、e.next=null
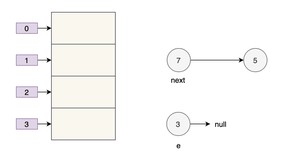
线程 B 开始执行,并且完成了数据转移。

此时,7 的 next 为 3,3 的 next 为 null。
随后线程 A 获得 CPU 时间片继续执行 ,将 3 放入新数组对应的位置,执行完此轮循环后线程 A 的情况如下:
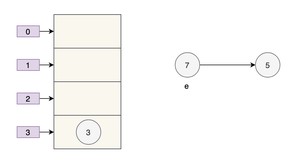
执行下一轮循环,此时 e=7,原本线程 A 中 7 的 next 为 5,但由于 table 是线程 A 和线程 B 共享的,而线程 B 顺利执行完后,7 的 next 变成了 3,那么此时线程 A 中,7 的 next 也为 3 了。
采用头部插入的方式,变成了下面这样子:
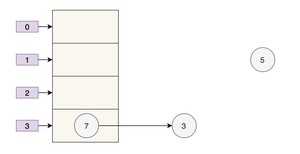
好像也没什么问题,此时 next = 3,e = 3。
进行下一轮循环,但此时,由于线程 B 将 3 的 next 变为了 null,所以此轮循环应该是最后一轮了。
接下来当执行完 即 3.next=7 后,3 和 7 之间就相互链接了,执行完 后,3 被头插法重新插入到链表中,执行结果如下图所示:
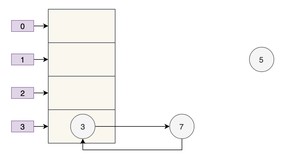
套娃开始,元素 5 也就成了弃婴,惨~~~
不过,JDK 8 时已经修复了这个问题,扩容时会保持链表原来的顺序(嗯,等于说了半天白说了,哈哈,这个面试题确实是这样,很水,但有些面试官又确实比较装逼)。
正常情况下,当发生哈希冲突时,HashMap 是这样的:
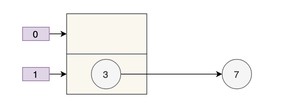
但多线程同时执行 put 操作时,如果计算出来的索引位置是相同的,那会造成前一个 key 被后一个 key 覆盖,从而导致元素的丢失。
put 的源码:
问题发生在步骤 ② 这里:
两个线程都执行了 if 语句,假设线程 A 先执行了 ,那 table 是这样的:
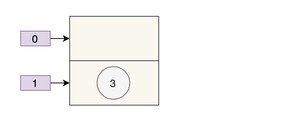
接着,线程 B 执行了 ,那 table 是这样的:
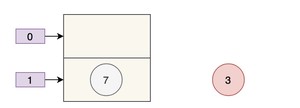
3 被干掉了。
线程 1 执行 put 时,因为元素个数超出阈值而导致出现扩容,线程 2 此时执行 get,就有可能出现这个问题。
因为线程 1 执行完 table = newTab 之后,线程 2 中的 table 此时也发生了变化,此时去 get 的时候当然会 get 到 null 了,因为元素还没有转移。
参考链接:
- https://blog.csdn.net/lonyw/article/details/
- https://zhuanlan.zhihu.com/p/
- https://www.zhihu.com/question/
- https://zhuanlan.zhihu.com/p/
HashMap 是线程不安全的主要是因为它在进行插入、删除和扩容等操作时可能会导致链表的结构发生变化,从而破坏了 HashMap 的不变性。具体来说,如果在一个线程正在遍历 HashMap 的链表时,另外一个线程对该链表进行了修改(比如添加了一个节点),那么就会导致链表的结构发生变化,从而破坏了当前线程正在进行的遍历操作,可能导致遍历失败或者出现死循环等问题。
为了解决这个问题,Java 提供了线程安全的 HashMap 实现类 ConcurrentHashMap。ConcurrentHashMap 内部采用了分段锁(Segment),将整个 Map 拆分为多个小的 HashMap,每个小的 HashMap 都有自己的锁,不同的线程可以同时访问不同的小 Map,从而实现了线程安全。在进行插入、删除和扩容等操作时,只需要锁住当前小 Map,不会对整个 Map 进行锁定,提高了并发访问的效率。
HashMap 是 Java 中最常用的集合之一,它是一种键值对存储的数据结构,可以根据键来快速访问对应的值。以下是对 HashMap 的总结:
- HashMap 采用数组+链表/红黑树的存储结构,能够在 O(1)的时间复杂度内实现元素的添加、删除、查找等操作。
- HashMap 是线程不安全的,因此在多线程环境下需要使用ConcurrentHashMap来保证线程安全。
- HashMap 的扩容机制是通过扩大数组容量和重新计算 hash 值来实现的,扩容时需要重新计算所有元素的 hash 值,因此在元素较多时扩容会影响性能。
- 在 Java 8 中,HashMap 的实现引入了拉链法、树化等机制来优化大量元素存储的情况,进一步提升了性能。
- HashMap 中的 key 是唯一的,如果要存储重复的 key,则后面的值会覆盖前面的值。
- HashMap 的初始容量和加载因子都可以设置,初始容量表示数组的初始大小,加载因子表示数组的填充因子。一般情况下,初始容量为 16,加载因子为 0.75。
- HashMap 在遍历时是无序的,因此如果需要有序遍历,可以使用TreeMap。
综上所述,HashMap 是一种高效的数据结构,具有快速查找和插入元素的能力,但需要注意线程安全和性能问题。
那如果大家已经掌握了 HashMap,那可以刷一下 LeetCode 的第 001 题、013 题,会用到 HashMap、数组和 for 循环,我把题解链接放在了技术派上:
- 二哥的 LeetCode 刷题笔记:001.两数之和
- 二哥的 LeetCode 刷题笔记:013.罗马数字转整数
另外,感谢球友踏歌对文章中的排版错误❎进行指正,文章已经进行了修改,感谢球友的支持。
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括 Java 基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM 等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 7600+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

这篇继续换个文风来写,给大家一点新鲜的空气。
俗话说了,“金无足赤人无完人”,HashMap 也不例外,有一种需求它就满足不了,假如我们需要一个按照插入顺序来排列的键值对集合,那 HashMap 就无能为力了。那该怎么办呢?必须得上今天这篇文章的主角:LinkedHashMap。
同学们好啊,还记得 HashMap 那篇吗?我自己感觉写得非常棒啊,既通俗易懂,又深入源码,真的是分析得透透彻彻、清清楚楚、明明白白的。(一不小心又甩了三个成语,有文化吧?)HashMap 哪哪都好,真的,只要你想用键值对,第一时间就应该想到它。
为了提高查找效率,HashMap 在插入的时候对键做了一次哈希算法,这就导致插入的元素是无序的。
对这一点还不太明白的同学,可以再回到 HashMap 那一篇,看看 hash 方法,再看看我对 方法的讲解,就能明白了,我们这里再来回顾一下。
其中这个公式 计算后的值就是键位在数组(桶)中的索引(下标/位置),但这它并不是按照 0、1、2、3、4、5 这样有序的下标将键值对插入到数组当中的,而是有一定的随机性。
比如说默认大小为 16 的 HashMap,如果 put 了 4 个键值对,可能下标是 0、4、9、11,那这样的话,在遍历 HashMap 的时候,就不一定能按照插入顺序来了。
看下面的例子。
来看输出结果
对比一下输出结果就可以看得出来,put 的时候是 沉默、王二、陈清扬的顺序,但遍历的时候就没有按照这个顺序来:沉默、陈清扬、王二,因为 HashMap 是无序的。
那怎么保证键值对的插入顺序呢?
LinkedHashMap 就是为这个需求应运而生的。LinkedHashMap 继承了 HashMap,所以 HashMap 有的关于键值对的功能,它也有了。
在此基础上,LinkedHashMap 内部追加了双向链表,来维护元素的插入顺序。注意下面代码中的 before 和 after,它俩就是用来维护当前元素的前一个元素和后一个元素的顺序的。
关于双向链表,同学们可以回头看一遍我写的 LinkedList 那篇文章,会对理解本篇的 LinkedHashMap 有很大的帮助。
用 LinkedHashMap 替换 HashMap,再来对比一下输出结果。
来看输出结果:
看,LinkedHashMap 是不是保持了插入顺序?这就对了。
在 HashMap 那篇文章里,我有讲解到一点,不知道同学们记不记得,就是 null 会插入到 HashMap 的第一位。
输出的结果是:
虽然 null 最后一位 put 进去的,但在遍历输出的时候,跑到了第一位。
那再来对比看一下 LinkedHashMap。
输出结果是:
null 在最后一位插入,在最后一位输出。
输出结果可以再次证明,HashMap 是无序的,LinkedHashMap 是可以维持插入顺序的。
那 LinkedHashMap 是如何做到这一点呢?我相信同学们和我一样,非常希望知道原因。
要想搞清楚,就需要深入研究一下 LinkedHashMap 的源码。LinkedHashMap 并未重写 HashMap 的 方法,而是重写了 方法需要调用的内部方法 。
这是 HashMap 的。
这是 LinkedHashMap 的。
前面曾提到 LinkedHashMap.Entry 继承了 HashMap.Node,并且追加了两个字段 before 和 after,用来维持键值对的关系。
在 LinkedHashMap 中,链表中的节点顺序是按照插入顺序维护的。当使用 put() 方法向 LinkedHashMap 中添加键值对时,会将新节点插入到链表的尾部,并更新 before 和 after 属性,以保证链表的顺序关系——由 方法来完成:
看到了吧,LinkedHashMap 在添加第一个元素的时候,会把 head 赋值为第一个元素,等到第二个元素添加进来的时候,会把第二个元素的 before 赋值为第一个元素,第一个元素的 afer 赋值为第二个元素。
这就保证了键值对是按照插入顺序排列的,明白了吧?
LinkedHashMap 不仅能够维持插入顺序,还能够维持访问顺序。访问包括调用 方法、 方法和 方法。
要维护访问顺序,需要我们在声明 LinkedHashMap 的时候指定三个参数。
第一个参数和第二个参数,看过 HashMap 的同学们应该很熟悉了,指的是初始容量和负载因子。
第三个参数如果为 true 的话,就表示 LinkedHashMap 要维护访问顺序;否则,维护插入顺序。默认是 false。
输出的结果如下所示:
当我们使用 方法访问键位“默”的元素后,输出结果中, 在最后;当我们访问键位“王”的元素后,输出结果中, 在最后, 在倒数第二位。
也就是说,最不经常访问的放在头部,这就有意思了。有意思在哪呢?
我们可以使用 LinkedHashMap 来实现 LRU 缓存,LRU 是 Least Recently Used 的缩写,即最近最少使用,是一种常用的页面置换算法,选择最近最久未使用的页面予以淘汰。
MyLinkedHashMap 是一个自定义类,它继承了 LinkedHashMap,并且重写了 方法——使 Map 最多可容纳 5 个元素,超出后就淘汰。
我们来测试一下。
输出结果如下所示:
和 依次被淘汰出局。
假如在 put “一枚有才华的程序员”之前 get 了键位为“默”的元素:
那输出结果就变了,对吧?
和 被淘汰出局了。
那 LinkedHashMap 是如何来维持访问顺序呢?同学们感兴趣的话,可以研究一下下面这三个方法。
会在调用 方法的时候被调用, 会在调用 方法的时候被调用, 会在调用 方法的时候被调用。
我来以 为例来讲解一下。
哪个元素被 get 就把哪个元素放在最后。了解了吧?
那同学们可能还想知道,为什么 LinkedHashMap 能实现 LRU 缓存,把最不经常访问的那个元素淘汰?
在插入元素的时候,需要调用 方法,该方法最后会调用 方法,这个方法被 LinkedHashMap 重写了。
方法会判断第一个元素是否超出了可容纳的最大范围,如果超出,那就会调用 方法对最不经常访问的那个元素进行删除。
由于 LinkedHashMap 要维护双向链表,所以 LinkedHashMap 在插入、删除操作的时候,花费的时间要比 HashMap 多一些。
这也是没办法的事,对吧,欲戴皇冠必承其重嘛。既然想要维护元素的顺序,总要付出点代价才行。
简单总结一下吧。
首先,我们知道 HashMap 是一种常用的哈希表数据结构,它可以快速地进行键值对的查找和插入操作。但是,HashMap 本身并不保证键值对的顺序,如果我们需要按照插入顺序或访问顺序来遍历键值对,就需要使用 LinkedHashMap 了。
LinkedHashMap 继承自 HashMap,它在 HashMap 的基础上,增加了一个双向链表来维护键值对的顺序。这个链表可以按照插入顺序或访问顺序排序,它的头节点表示最早插入或访问的元素,尾节点表示最晚插入或访问的元素。这个链表的作用就是让 LinkedHashMap 可以保持键值对的顺序,并且可以按照顺序遍历键值对。
LinkedHashMap 还提供了两个构造方法来指定排序方式,分别是按照插入顺序排序和按照访问顺序排序。在按照访问顺序排序的情况下,每次访问一个键值对,都会将该键值对移到链表的尾部,以保证最近访问的元素在最后面。如果需要删除最早加入的元素,可以通过重写 removeEldestEntry() 方法来实现。
总之,LinkedHashMap 通过维护一个双向链表来保持键值对的顺序,可以按照插入顺序或访问顺序来遍历键值对。如果你需要按照顺序来遍历键值对,那么 LinkedHashMap 就是你的不二选择了!
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括Java基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 10000+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

下面有请王老师上台,来给大家讲一讲 TreeMap,鼓掌了!
之前 LinkedHashMap 那篇文章里提到过了,HashMap 是无序的,所以有了 LinkedHashMap,加上了双向链表后,就可以保持元素的插入顺序和访问顺序,那 TreeMap 呢?
TreeMap 由红黑树实现,可以保持元素的自然顺序,或者实现了 Comparator 接口的自定义顺序。
可能有些同学不了解红黑树,我这里来普及一下:
红黑树(英语:Red–black tree)是一种自平衡的二叉查找树(Binary Search Tree),结构复杂,但却有着良好的性能,完成查找、插入和删除的时间复杂度均为 log(n)。
二叉查找树是一种常见的树形结构,它的每个节点都包含一个键值对。每个节点的左子树节点的键值小于该节点的键值,右子树节点的键值大于该节点的键值,这个特性使得二叉查找树非常适合进行数据的查找和排序操作。
下面是一个简单的手绘图,展示了一个二叉查找树的结构:
在上面这个二叉查找树中,根节点是 8,左子树节点包括 3、1、6、4 和 7,右子树节点包括 10、14 和 13。
- 3<8<10
- 1<3<6
- 4<6<7
- 10<14
- 13<14
这是一颗典型的二叉查找树:
- 1)左子树上所有节点的值均小于或等于它的根结点的值。
- 2)右子树上所有节点的值均大于或等于它的根结点的值。
- 3)左、右子树也分别为二叉查找树。
二叉查找树用来查找非常方面,从根节点开始遍历,如果当前节点的键值等于要查找的键值,则查找成功;如果要查找的键值小于当前节点的键值,则继续遍历左子树;如果要查找的键值大于当前节点的键值,则继续遍历右子树。如果遍历到叶子节点仍然没有找到,则查找失败。
插入操作也非常简单,从根节点开始遍历,如果要插入的键值小于当前节点的键值,则将其插入到左子树中;如果要插入的键值大于当前节点的键值,则将其插入到右子树中。如果要插入的键值已经存在于树中,则更新该节点的值。
删除操作稍微复杂一些,需要考虑多种情况,包括要删除的节点是叶子节点、要删除的节点只有一个子节点、要删除的节点有两个子节点等等。
总之,二叉查找树是一种非常常用的数据结构,它可以帮助我们实现数据的查找、排序和删除等操作。
理解二叉查找树了吧?
不过,二叉查找树有一个明显的不足,就是容易变成瘸子,就是一侧多,一侧少,比如说这样:
在上面这个不平衡的二叉查找树中,左子树比右子树高。根节点是 6,左子树节点包括 4、3 和 1,右子树节点包括 8、7 和 9。
由于左子树比右子树高,这个不平衡的二叉查找树可能会导致查找、插入和删除操作的效率下降。
来一个更极端的情况。
在上面这个极度不平衡的二叉查找树中,所有节点都只有一个右子节点,根节点是 1,右子树节点包括 2、3、4、5 和 6。
这种极度不平衡的二叉查找树会导致查找、插入和删除操作的效率急剧下降,因为每次操作都只能在右子树中进行,而左子树几乎没有被利用到。
查找的效率就要从 log(n) 变成 o(n) 了(戳这里了解时间复杂度),对吧?
必须要平衡一下,对吧?于是就有了平衡二叉树,左右两个子树的高度差的绝对值不超过 1,就像下图这样:
根节点是 8,左子树节点包括 4、2、6、5 和 7,右子树节点包括 12、10、14、13 和 15。左子树和右子树的高度差不超过1,因此它是一个平衡二叉查找树。
平衡二叉树就像是一棵树形秤,它的左右两边的重量要尽可能的平衡。当我们往平衡二叉树中插入一个节点时,平衡二叉树会自动调整节点的位置,以保证树的左右两边的高度差不超过1。类似地,当我们删除一个节点时,平衡二叉树也会自动调整节点的位置,以保证树的左右两边的高度差不超过1。
常见的平衡二叉树包括AVL树、红黑树等等,它们都是通过旋转操作来调整树的平衡,使得左子树和右子树的高度尽可能接近。
AVL树的示意图:
AVL树是一种高度平衡的二叉查找树,它要求左子树和右子树的高度差不超过1。由于AVL树的平衡度比较高,因此在进行插入和删除操作时需要进行更多的旋转操作来保持平衡,但是在查找操作时效率较高。AVL树适用于读操作比较多的场景。
例如,对于一个需要频繁进行查找操作的场景,如字典树、哈希表等数据结构,可以使用AVL树来进行优化。另外,AVL树也适用于需要保证数据有序性的场景,如数据库中的索引。
AVL树最初由两位苏联的计算机科学家,Adelson-Velskii和Landis,于1962年提出。因此,AVL树就以他们两人名字的首字母缩写命名了。
AVL树的发明对计算机科学的发展有着重要的影响,不仅为后来的平衡二叉树提供了基础,而且为其他领域的数据结构和算法提供了启示。
红黑树的示意图(R 即 Red「红」、B 即 Black「黑」):
红黑树,顾名思义,就是节点是红色或者黑色的平衡二叉树,它通过颜色的约束来维持二叉树的平衡,它要求任意一条路径上的黑色节点数目相同,同时还需要满足一些其他特定的条件,如红色节点的父节点必须为黑色节点等。
- 1)每个节点都只能是红色或者黑色
- 2)根节点是黑色
- 3)每个叶节点(NIL 节点,空节点)是黑色的。
- 4)如果一个节点是红色的,则它两个子节点都是黑色的。也就是说在一条路径上不能出现相邻的两个红色节点。
- 5)从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
由于红黑树的平衡度比AVL树稍低,因此在进行插入和删除操作时需要进行的旋转操作较少,但是在查找操作时效率仍然较高。红黑树适用于读写操作比较均衡的场景。
那,关于红黑树,同学们就先了解到这,脑子里有个大概的印象,知道 TreeMap 是个什么玩意。
默认情况下,TreeMap 是根据 key 的自然顺序排列的。比如说整数,就是升序,1、2、3、4、5。
输出结果如下所示:
TreeMap 是怎么做到的呢?想一探究竟,就得上源码了,来看 TreeMap 的 方法:
- 首先定义一个Entry类型的变量t,用于表示当前的根节点;
- 如果t为null,说明TreeMap为空,直接创建一个新的节点作为根节点,并将size设置为1;
- 如果t不为null,说明需要在TreeMap中查找键所对应的节点。因为TreeMap中的元素是有序的,所以可以使用二分查找的方式来查找节点;
- 如果TreeMap中使用了Comparator来进行排序,则使用Comparator进行比较,否则使用Comparable进行比较。如果查找到了相同的键,则直接更新键所对应的值;
- 如果没有查找到相同的键,则创建一个新的节点,并将其插入到TreeMap中。然后使用fixAfterInsertion()方法来修正插入节点后的平衡状态;
- 最后将TreeMap的size加1,然后返回null。如果更新了键所对应的值,则返回原先的值。
注意 这行代码,就是用来进行 key 比较的,由于此时 key 是 String,所以就会调用 String 类的 方法进行比较。
来看下面的示例。
输出结果如下所示:
从结果可以看得出,是按照字母的升序进行排序的。
如果自然顺序不满足,那就可以在声明 TreeMap 对象的时候指定排序规则。
TreeMap 提供了可以指定排序规则的构造方法:
返回的是 Collections.ReverseComparator 对象,就是用来反转顺序的,非常方便。
所以,输出结果如下所示:
HashMap 是无序的,插入的顺序随着元素的增加会不停地变动。但 TreeMap 能够至始至终按照指定的顺序排列,这对于需要自定义排序的场景,实在是太有用了!
既然 TreeMap 的元素是经过排序的,那找出最大的那个,最小的那个,或者找出所有大于或者小于某个值的键来说,就方便多了。
TreeMap 考虑得很周全,恰好就提供了 、 这样获取最后一个 key 和第一个 key 的方法。
获取的是到指定 key 之前的 key; 获取的是指定 key 之后的 key(包括指定 key)。
来看一下输出结果:
再来看一下例子:
headMap、tailMap、subMap方法分别获取了小于3、大于等于4、大于等于2且小于4的键值对。
在学习 TreeMap 之前,我们已经学习了 HashMap 和 LinkedHashMap ,那如何从它们三个中间选择呢?
需要考虑以下因素:
- 是否需要按照键的自然顺序或者自定义顺序进行排序。如果需要按照键排序,则可以使用 TreeMap;如果不需要排序,则可以使用 HashMap 或 LinkedHashMap。
- 是否需要保持插入顺序。如果需要保持插入顺序,则可以使用 LinkedHashMap;如果不需要保持插入顺序,则可以使用 TreeMap 或 HashMap。
- 是否需要高效的查找。如果需要高效的查找,则可以使用 LinkedHashMap 或 HashMap,因为它们的查找操作的时间复杂度为 O(1),而是 TreeMap 是 O(log n)。
LinkedHashMap 内部使用哈希表来存储键值对,并使用一个双向链表来维护插入顺序,但查找操作只需要在哈希表中进行,与链表无关,所以时间复杂度为 O(1)
来个表格吧,一目了然。
好了,下课,关于 TreeMap 我们就讲到这里吧,希望同学们都能对 TreeMap 有一个清晰的认识。我们下节课见~
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括Java基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 10000+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

好,我们这节继续有请王老师上台来给大家讲 ArrayDeque,鼓掌欢迎了👏🏻。
Java 里有一个叫做Stack的类,却没有叫做Queue的类(它只是个接口名字,和类还不一样)。
当需要使用栈时,Java 已不推荐使用Stack,而是推荐使用更高效的ArrayDeque(双端队列),原因我们第一次讲集合框架的时候,其实已经聊过了,Stack 是一个“原始”类,它的核心方法上都加了 关键字以确保线程安全,当我们不需要线程安全(比如说单线程环境下)性能就会比较差。
也就是说,当需要使用栈时候,请首选ArrayDeque。
在上面的示例中,我们先创建了一个 ArrayDeque 对象,然后使用 push 方法向栈中添加了三个元素。接着使用 peek 方法获取栈顶元素,使用 pop 方法弹出栈顶元素,使用 pop 和 push 方法修改栈顶元素,使用迭代器查找元素在栈中的位置。
ArrayDeque 又实现了 Deque 接口(Deque 又实现了 Queue 接口):
因此,当我们需要使用队列的时候,也可以选择 ArrayDeque。
在上面的示例中,我们先创建了一个 ArrayDeque 对象,然后使用 offer 方法向队列中添加了三个元素。接着使用 peek 方法获取队首元素,使用 poll 方法弹出队首元素,使用 poll 和 offer 方法修改队列中的元素,使用迭代器查找元素在队列中的位置。
我们前面讲了,LinkedList不只是个 List,还是一个 Queue,它也实现了 Deque 接口。
所以,当我们需要使用队列时,还可以选择LinkedList。
在使用 LinkedList 作为队列时,可以使用 offer() 方法将元素添加到队列的末尾,使用 poll() 方法从队列的头部删除元素,使用迭代器或者 poll() 方法依次遍历元素。
要讲栈和队列,首先要讲Deque接口。Deque的含义是“double ended queue”,即双端队列,它既可以当作栈使用,也可以当作队列使用。下表列出了Deque与Queue相对应的接口:
下表列出了Deque与Stack对应的接口:
上面两个表共定义了Deque的 12 个接口。
添加,删除,取值都有两套接口,它们功能相同,区别是对失败情况的处理不同。
一套接口遇到失败就会抛出异常,另一套遇到失败会返回特殊值(或)。除非某种实现对容量有限制,大多数情况下,添加操作是不会失败的。
虽然Deque的接口有 12 个之多,但无非就是对容器的两端进行操作,或添加,或删除,或查看。明白了这一点讲解起来就会非常简单。
ArrayDeque和LinkedList是Deque的两个通用实现,由于官方更推荐使用ArrayDeque用作栈和队列,加之上一篇已经讲解过LinkedList,本文将着重讲解ArrayDeque的具体实现。
从名字可以看出ArrayDeque底层通过数组实现,为了满足可以同时在数组两端插入或删除元素的需求,该数组还必须是循环的,即循环数组(circular array),也就是说数组的任何一点都可能被看作起点或者终点。
ArrayDeque是非线程安全的(not thread-safe),当多个线程同时使用的时候,需要手动同步;另外,该容器不允许放入元素。
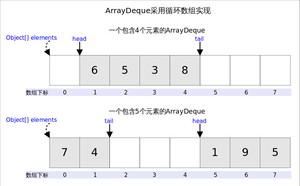
上图中我们看到,指向首端第一个有效元素,指向尾端第一个可以插入元素的空位。因为是循环数组,所以不一定总等于 0,也不一定总是比大。
的作用是在Deque的首端插入元素,也就是在的前面插入元素,在空间足够且下标没有越界的情况下,只需要将即可。

实际需要考虑:
- 空间是否够用,以及
- 下标是否越界的问题。
上图中,如果为之后接着调用,虽然空余空间还够用,但为,下标越界了。下列代码很好的解决了这两个问题。
上述代码我们看到,空间问题是在插入之后解决的,因为总是指向下一个可插入的空位,也就意味着数组至少有一个空位,所以插入元素的时候不用考虑空间问题。
下标越界的处理解决起来非常简单,就可以了,这段代码相当于取余,同时解决了为负值的情况。因为必需是的指数倍,就是二进制低位全,跟相与之后就起到了取模的作用,如果为负数(其实只可能是-1),则相当于对其取相对于的补码。
下面再说说扩容函数,其逻辑是申请一个更大的数组(原数组的两倍),然后将原数组复制过去。过程如下图所示:
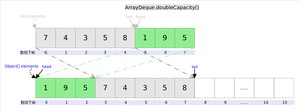
图中我们看到,复制分两次进行,第一次复制右边的元素,第二次复制左边的元素。
该方法的实现中,首先检查 head 和 tail 是否相等,如果不相等则抛出异常。然后计算出 head 右边的元素个数 r,以及新的容量 newCapacity,如果 newCapacity 太大则抛出异常。
接下来创建一个新的 Object 数组 a,将原有 ArrayDeque 中 head 右边的元素复制到 a 的前面(即图中绿色部分),将 head 左边的元素复制到 a 的后面(即图中灰色部分)。最后将 elements 数组替换为 a,head 设置为 0,tail 设置为 n(即新容量的长度)。
需要注意的是,由于 elements 数组被替换为 a 数组,因此在方法调用结束后,原有的 elements 数组将不再被引用,会被垃圾回收器回收。
的作用是在Deque的尾端插入元素,也就是在的位置插入元素,由于总是指向下一个可以插入的空位,因此只需要即可。插入完成后再检查空间,如果空间已经用光,则调用进行扩容。

下标越界处理方式中已经讲过,不再赘述。
的作用是删除并返回Deque首端元素,也即是位置处的元素。如果容器不空,只需要直接返回即可,当然还需要处理下标的问题。由于中不允许放入,当时,意味着容器为空。
的作用是删除并返回Deque尾端元素,也即是位置前面的那个元素。
的作用是返回但不删除Deque首端元素,也即是位置处的元素,直接返回即可。
的作用是返回但不删除Deque尾端元素,也即是位置前面的那个元素。
当需要实现先进先出(FIFO)或者先进后出(LIFO)的数据结构时,可以考虑使用 ArrayDeque。以下是一些使用 ArrayDeque 的场景:
- 管理任务队列:如果需要实现一个任务队列,可以使用 ArrayDeque 来存储任务元素。在队列头部添加新任务元素,从队列尾部取出任务进行处理,可以保证任务按照先进先出的顺序执行。
- 实现栈:ArrayDeque 可以作为栈的实现方式,支持 push、pop、peek 等操作,可以用于需要后进先出的场景。
- 实现缓存:在需要缓存一定数量的数据时,可以使用 ArrayDeque。当缓存的数据量超过容量时,可以从队列头部删除最老的数据,从队列尾部添加新的数据。
- 实现事件处理器:ArrayDeque 可以作为事件处理器的实现方式,支持从队列头部获取事件进行处理,从队列尾部添加新的事件。
简单总结一下吧。
ArrayDeque 是 Java 标准库中的一种双端队列实现,底层基于数组实现。与 LinkedList 相比,ArrayDeque 的性能更优,因为它使用连续的内存空间存储元素,可以更好地利用 CPU 缓存,在大多数情况下也更快。
为什么这么说呢?
因为ArrayDeque 的底层实现是数组,而 LinkedList 的底层实现是链表。数组是一段连续的内存空间,而链表是由多个节点组成的,每个节点存储数据和指向下一个节点的指针。因此,在使用 LinkedList 时,需要频繁进行内存分配和释放,而 ArrayDeque 在创建时就一次性分配了连续的内存空间,不需要频繁进行内存分配和释放,这样可以更好地利用 CPU 缓存,提高访问效率。
现代计算机CPU对于数据的局部性有很强的依赖,如果需要访问的数据在内存中是连续存储的,那么就可以利用CPU的缓存机制,提高访问效率。而当数据存储在不同的内存块里时,每次访问都需要从内存中读取,效率会受到影响。
当然了,使用 ArrayDeque 时,数组复制操作也是需要考虑的性能消耗之一。
当 ArrayDeque 的元素数量超过了初始容量时,会触发扩容操作。扩容操作会创建一个新的数组,并将原有元素复制到新数组中。扩容操作的时间复杂度为 O(n)。
不过,ArrayDeque 的扩容策略(当 ArrayDeque 中的元素数量达到数组容量时,就需要进行扩容操作,扩容时会将数组容量扩大为原来的两倍)可以在一定程度上减少数组复制的次数和时间消耗,同时保证 ArrayDeque 的性能和空间利用率。
ArrayDeque 不仅支持常见的队列操作,如添加元素、删除元素、获取队列头部元素、获取队列尾部元素等。同时,它还支持栈操作,如 push、pop、peek 等。这使得 ArrayDeque 成为一种非常灵活的数据结构,可以用于各种场景的数据存储和处理。
参考链接:https://github.com/CarpenterLee/JCFInternals,作者:李豪,整理:沉默王二
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括Java基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 10000+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

继续有请王老师,来上台给大家讲讲优先级队列 PriorityQueue。
PriorityQueue 是 Java 中的一个基于优先级堆的优先队列实现,它能够在 O(log n) 的时间复杂度内实现元素的插入和删除操作,并且能够自动维护队列中元素的优先级顺序。
通俗来说,PriorityQueue 就是一个队列,但是它不是先进先出的,而是按照元素优先级进行排序的。当你往 PriorityQueue 中插入一个元素时,它会自动根据元素的优先级将其插入到合适的位置。当你从 PriorityQueue 中删除一个元素时,它会自动将优先级最高的元素出队。
下面👇🏻是一个简单的PriorityQueue示例:
在上述代码中,我们首先创建了一个 PriorityQueue 对象,并向其中添加了三个元素。然后,我们使用 while 循环遍历 PriorityQueue 中的元素,并打印出来。来看输出结果:
再来看一下示例。
在上述代码中,我们使用了 Comparator.reverseOrder() 方法指定了 PriorityQueue 的优先级顺序为降序。也就是说,PriorityQueue 中的元素会按照从大到小的顺序排序。
其他部分的代码与之前的例子相同,我们再来看一下输出结果:
对比一下两个例子的输出结果,不难发现,顺序正好相反。
PriorityQueue 的主要作用是维护一组数据的排序,使得取出数据时可以按照一定的优先级顺序进行,当我们调用 poll() 方法时,它会从队列的顶部弹出最高优先级的元素。它在很多场景下都有广泛的应用,例如任务调度、事件处理等场景,以及一些算法中需要对数据进行排序的场景。
在实际应用中,PriorityQueue 也经常用于实现 Dijkstra 算法、Prim 算法、Huffman 编码等算法。这里简单说一下这几种算法的作用,理解不了也没关系哈。
Dijkstra算法是一种用于计算带权图中的最短路径的算法。该算法采用贪心的策略,在遍历图的过程中,每次选取当前到源点距离最短的一个顶点,并以它为中心进行扩展,更新其他顶点的距离值。经过多次扩展,可以得到源点到其它所有顶点的最短路径。
Prim算法是一种用于求解最小生成树的算法,可以在加权连通图中找到一棵生成树,使得这棵生成树的所有边的权值之和最小。该算法从任意一个顶点开始,逐渐扩展生成树的规模,每次选择一个距离已生成树最近的顶点加入到生成树中。
Huffman编码是一种基于霍夫曼树的压缩算法,用于将一个字符串转换为二进制编码以进行压缩。该算法的主要思想是通过建立霍夫曼树,将出现频率较高的字符用较短的编码表示,而出现频率较低的字符用较长的编码表示,从而实现对字符串的压缩。在解压缩时,根据编码逐步解析出原字符串。
由于 PriorityQueue 的底层是基于堆实现的,因此在数据量比较大时,使用 PriorityQueue 可以获得较好的时间复杂度。
这里牵涉到了大小关系,元素大小的评判可以通过元素本身的自然顺序(natural ordering),也可以通过构造时传入的比较器(Comparator,或者元素自身实现 Comparable 接口)来决定。
在 PriorityQueue 中,每个元素都有一个优先级,这个优先级决定了元素在队列中的位置。队列内部通过小顶堆(也可以是大顶堆)的方式来维护元素的优先级关系。具体来说,小顶堆是一个完全二叉树,任何一个非叶子节点的权值,都不大于其左右子节点的权值,这样保证了队列的顶部元素(堆顶)一定是优先级最高的元素。
完全二叉树(Complete Binary Tree)是一种二叉树,其中除了最后一层,其他层的节点数都是满的,最后一层的节点都靠左对齐。下面是一个完全二叉树的示意图:
堆是一种完全二叉树,堆的特点是根节点的值最小(小顶堆)或最大(大顶堆),并且任意非根节点i的值都不大于(或不小于)其父节点的值。
这是一颗包含整数 1, 2, 3, 4, 5, 6, 7 的小顶堆:
这是一颗大顶堆。
因为完全二叉树的结构比较规则,所以可以使用数组来存储堆的元素,而不需要使用指针等额外的空间。
在堆中,每个节点的下标和其在数组中的下标是一一对应的,假设节点下标为i,则其父节点下标为i/2,其左子节点下标为2i,其右子节点下标为2i+1。
假设有一个数组arr=[10, 20, 15, 30, 40],现在要将其转化为一个小顶堆。
首先,我们将数组按照完全二叉树的形式排列,如下图所示:
从上往下、从左往右依次给每个节点编号,如下所示:
接下来,我们按照上述公式,依次确定每个节点在数组中的位置。例如,节点1的父节点下标为1/2=0,左子节点下标为2*1=2,右子节点下标为2*1+1=3,因此节点1在数组中的位置为0,节点2在数组中的位置为2,节点3在数组中的位置为3。
对应的数组为[10, 20, 15, 30, 40],符合小顶堆的定义,即每个节点的值都小于或等于其子节点的值。
好,我们画幅图再来理解一下。
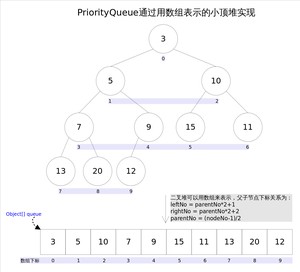
上图中我们给每个元素按照层序遍历的方式进行了编号,如果你足够细心,会发现父节点和子节点的编号是有联系的,更确切的说父子节点的编号之间有如下关系:
通过上述三个公式,可以轻易计算出某个节点的父节点以及子节点的下标。这也就是为什么可以直接用数组来存储堆的原因。
和的语义相同,都是向优先队列中插入元素,只是接口规定二者对插入失败时的处理不同,前者在插入失败时抛出异常,后则则会返回。对于PriorityQueue这两个方法其实没什么差别。
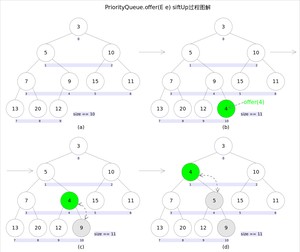
新加入的元素可能会破坏小顶堆的性质,因此需要进行必要的调整。
上述代码中,扩容函数类似于里的函数,就是再申请一个更大的数组,并将原数组的元素复制过去,这里不再赘述。需要注意的是方法,该方法用于插入元素并维持堆的特性。
调整的过程为:从指定的位置开始,将逐层与当前点的进行比较并交换,直到满足为止。注意这里的比较可以是元素的自然顺序,也可以是依靠比较器的顺序。
和的语义完全相同,都是获取但不删除队首元素,也就是队列中权值最小的那个元素,二者唯一的区别是当方法失败时前者抛出异常,后者返回。根据小顶堆的性质,堆顶那个元素就是全局最小的那个;由于堆用数组表示,根据下标关系,下标处的那个元素既是堆顶元素。所以直接返回数组下标处的那个元素即可。
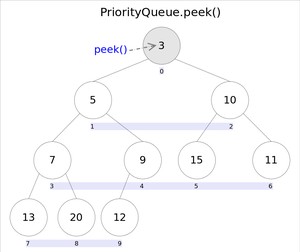
代码也就非常简洁:
和方法的语义也完全相同,都是获取并删除队首元素,区别是当方法失败时前者抛出异常,后者返回。由于删除操作会改变队列的结构,为维护小顶堆的性质,需要进行必要的调整。
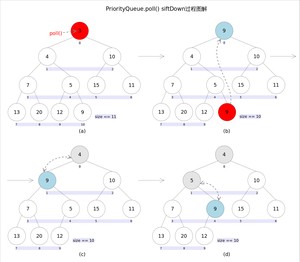
代码如下:
上述代码首先记录下标处的元素,并用最后一个元素替换下标位置的元素,之后调用方法对堆进行调整,最后返回原来下标处的那个元素(也就是最小的那个元素)。重点是方法,该方法的作用是从指定的位置开始,将逐层向下与当前点的左右孩子中较小的那个交换,直到小于或等于左右孩子中的任何一个为止。
方法用于删除队列中跟相等的某一个元素(如果有多个相等,只删除一个),该方法不是Queue接口内的方法,而是Collection接口的方法。由于删除操作会改变队列结构,所以要进行调整;又由于删除元素的位置可能是任意的,所以调整过程比其它方法稍加繁琐。
具体来说,可以分为 2 种情况:
- 删除的是最后一个元素。直接删除即可,不需要调整。
- 删除的不是最后一个元素,从删除点开始以最后一个元素为参照调用一次即可。此处不再赘述。
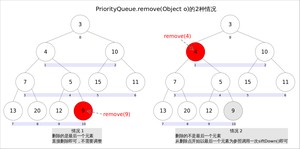
具体代码如下:
PriorityQueue 是一个非常常用的数据结构,它是一种特殊的堆(Heap)实现,可以用来高效地维护一个有序的集合。
- 它的底层实现是一个数组,通过堆的性质来维护元素的顺序。
- 取出元素时按照优先级顺序(从小到大或者从大到小)进行取出。
- 如果需要指定排序,元素必须实现 Comparable 接口或者传入一个 Comparator 来进行比较。
可以通过 LeetCode 的第 23 题:合并K个升序链表 来练习 PriorityQueue 的使用。
我把题解已经放到了技术派中,大家可以去作为参考。
合并K个升序链表
参考链接:https://github.com/CarpenterLee/JCFInternals,作者:李豪,整理:沉默王二
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括Java基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 10000+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

“二哥,为什么要讲时间复杂度呀?”三妹问。
“因为接下来要用到啊。后面我们学习 ArrayList、LinkedList 的时候,会比较两者在增删改查时的执行效率,而时间复杂度是衡量执行效率的一个重要标准。”我说。
“到时候跑一下代码,统计一下前后的时间差不更准确吗?”三妹反问道。
“实际上,你说的是另外一种评估方法,这种评估方法可以得出非常准确的数值,但也有很大的局限性。”我不急不慢地说。
第一,测试结果会受到测试环境的影响。你比如说,同样的代码,在我这台 iMac 上跑出来的时间和在你那台华为的 MacBook 上跑出的时间可能就差别很大。
第二,测试结果会受到测试数据的影响。你比如说,一个排序后的数组和一个没有排序后的数组,调用了同一个查询方法,得出来的结果可能会差别特别大。
“因此,我们需要这种不依赖于具体测试环境和测试数据就能粗略地估算出执行效率的方法,时间复杂度就是其中的一种,还有一种是空间复杂度。”我继续补充道,“如果你后面刷 LeetCode的话,对时间复杂度这个概念也会比较依赖。”
来看下面这段代码:
这段代码非常简单,方法体里总共 5 行代码,包括“}”那一行。每段代码的执行时间可能都不大一样,但假设我们认为每行代码的执行时间是一样的,比如说 unit_time,那么这段代码总的执行时间为多少呢?
“这个我知道呀!”三妹喊道,“第 1、5 行需要 2 个 unit_time,第 2、3 行需要 2nunit_time,总的时间就是 2(n+1)*unit_time。”
“对,一段代码的执行时间 T(n) 和总的执行次数成正比,也就是说,代码执行的次数越多,花费的时间就越多。”我总结道,“这个规律可以用一个公式来表达:”
T(n) = O(f(n))
f(n) 表示代码总的执行次数,大写 O 表示代码的执行时间 T(n) 和 f(n) 成正比。
这也就是大 O 表示法,它不关心代码具体的执行时间是多少,它关心的是代码执行时间的变化趋势,这也就是时间复杂度这个概念的由来。
对于上面那段代码 来说,影响时间复杂度的主要是第 2 行代码,其余的,像系数 2、常数 2 都是可以忽略不计的,我们只关心影响最大的那个,所以时间复杂度就表示为 。
常见的时间复杂度有这么 3 个:
代码的执行时间,和数据规模 n 没有多大关系。
括号中的 1 可以是 3,可以是 5,可以 100,我们习惯用 1 来表示,表示这段代码的执行时间是一个常数级别。比如说下面这段代码:
实际上执行了 3 次,但我们也认为这段代码的时间复杂度为 。
再举一个简单的例子。当我们访问数组中的一个元素时,它的时间复杂度就是常数时间复杂度 O(1)。
时间复杂度和数据规模 n 是线性关系。换句话说,数据规模增大 K 倍,代码执行的时间就大致增加 K 倍。
当我们遍历一个数组时,它的时间复杂度就是线性时间复杂度 O(n)。
时间复杂度和数据规模 n 是对数关系。换句话说,数据规模大幅增加时,代码执行的时间只有少量增加。
来看一下代码示例,
换句话说,当数据量 n 从 2 增加到 2^64 时,代码执行的时间只增加了 64 倍。
再举个例子。当我们对一个已排序的数组进行二分查找时,它的时间复杂度就是对数时间复杂度 O(log n)。
当我们对一个数组进行嵌套循环时,它的时间复杂度就是平方时间复杂度 O(n^2)。
当我们递归求解一个问题时,每一次递归都会分成两个子问题,这种情况下,它的时间复杂度就是指数时间复杂度 O(2^n)。
上面的代码是递归求解斐波那契数列的方法,它的时间复杂度是指数级别的。
“好了,三妹,这节就讲到这吧,理解了上面 5 个时间复杂度,后面我们学习 ArrayList、LinkedList 的时候,两者在增删改查时的执行效率就很容易对比清楚了。”我伸了个懒腰后对三妹说。
“好的,二哥。”三妹重新回答沙发上,一盘王者荣耀即将开始。
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括Java基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 10000+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

“终于,二哥,我们要聊 LinkedList 和 ArrayList 之间的差别了,我期待了很久。”三妹嘟囔着说。
“其实经过前面两节的分析,差别已经很清晰了。”我喃喃道。
“哥,你再说点吧,深挖一下,OK?”
“好吧,那就让我们出发吧!”
PS:为了和前面两节的源码做适当的区分,这里采用的是 Java 11 的源码,请务必注意。但整体上差别很小。
ArrayList 实现了 List 接口,继承了 AbstractList 抽象类。
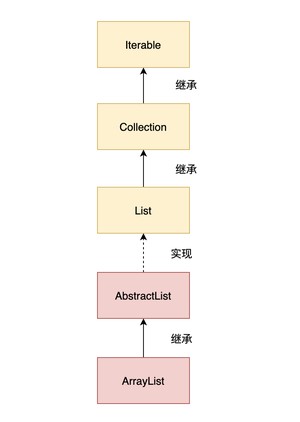
底层是基于数组实现的,并且实现了动态扩容(当需要添加新元素时,如果 elementData 数组已满,则会自动扩容,新的容量将是原来的 1.5 倍),来看一下 ArrayList 的部分源码。
ArrayList 还实现了 RandomAccess 接口,这是一个标记接口:
内部是空的,标记“实现了这个接口的类支持快速(通常是固定时间)随机访问”。快速随机访问是什么意思呢?就是说不需要遍历,就可以通过下标(索引)直接访问到内存地址。而 LinkedList 没有实现该接口,表示它不支持高效的随机访问,需要通过遍历来访问元素。
ArrayList 还实现了 Cloneable 接口,这表明 ArrayList 是支持拷贝的。ArrayList 内部的确也重写了 Object 类的 方法。
ArrayList 还实现了 Serializable 接口,同样是一个标记接口:
内部也是空的,标记“实现了这个接口的类支持序列化”。序列化是什么意思呢?Java 的序列化是指,将对象转换成以字节序列的形式来表示,这些字节序中包含了对象的字段和方法。序列化后的对象可以被写到数据库、写到文件,也可用于网络传输。
眼睛雪亮的小伙伴可能会注意到,ArrayList 中的关键字段 elementData 使用了 transient 关键字修饰,这个关键字的作用是,让它修饰的字段不被序列化。
这不前后矛盾吗?一个类既然实现了 Serilizable 接口,肯定是想要被序列化的,对吧?那为什么保存关键数据的 elementData 又不想被序列化呢?
这还得从 “ArrayList 是基于数组实现的”开始说起。大家都知道,数组是定长的,就是说,数组一旦声明了,长度(容量)就是固定的,不能像某些东西一样伸缩自如。这就很麻烦,数组一旦装满了,就不能添加新的元素进来了。
ArrayList 不想像数组这样活着,它想能屈能伸,所以它实现了动态扩容。一旦在添加元素的时候,发现容量用满了 ,就按照原来数组的 1.5 倍()进行扩容。扩容之后,再将原有的数组复制到新分配的内存地址上 。
这部分源码我们在之前讲 ArrayList 的时候就已经讲的很清楚了,这里就一笔带过。
动态扩容意味着什么?
意味着数组的实际大小可能永远无法被填满的,总有多余出来空置的内存空间。
比如说,默认的数组大小是 10,当添加第 11 个元素的时候,数组的长度扩容了 1.5 倍,也就是 15,意味着还有 4 个内存空间是闲置的,对吧?
序列化的时候,如果把整个数组都序列化的话,是不是就多序列化了 4 个内存空间。当存储的元素数量非常非常多的时候,闲置的空间就非常非常大,序列化耗费的时间就会非常非常多。
于是,ArrayList 做了一个愉快而又聪明的决定,内部提供了两个私有方法 writeObject 和 readObject 来完成序列化和反序列化。
从 writeObject 方法的源码中可以看得出,它使用了 ArrayList 的实际大小 size 而不是数组的长度()来作为元素的上限进行序列化。
此处应该有掌声啊!不是为我,为 Java 源码的作者们,他们真的是太厉害了,可以用两个词来形容他们——殚精竭虑、精益求精。
666
这是readObject方法的源码:
LinkedList 是一个继承自 AbstractSequentialList 的双向链表,因此它也可以被当作堆栈、队列或双端队列进行操作。
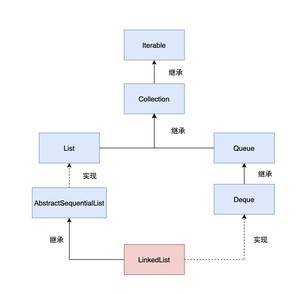
来看一下部分源码:
LinkedList 内部定义了一个 Node 节点,它包含 3 个部分:元素内容 item,前引用 prev 和后引用 next。这个在讲 LinkedList 的时候也讲过了,这里略过。
LinkedList 还实现了 Cloneable 接口,这表明 LinkedList 是支持拷贝的。
LinkedList 还实现了 Serializable 接口,这表明 LinkedList 是支持序列化的。眼睛雪亮的小伙伴可能又注意到了,LinkedList 中的关键字段 size、first、last 都使用了 transient 关键字修饰,这不又矛盾了吗?到底是想序列化还是不想序列化?
答案是 LinkedList 想按照自己的方式序列化,来看它自己实现的 方法:
发现没?LinkedList 在序列化的时候只保留了元素的内容 item,并没有保留元素的前后引用。这样就节省了不少内存空间,对吧?
那有些小伙伴可能就疑惑了,只保留元素内容,不保留前后引用,那反序列化的时候怎么办?
注意 for 循环中的 方法,它可以把链表重新链接起来,这样就恢复了链表序列化之前的顺序。很妙,对吧?
和 ArrayList 相比,LinkedList 没有实现 RandomAccess 接口,这是因为 LinkedList 存储数据的内存地址是不连续的,所以不支持随机访问。
前面我们已经从多个维度了解了 ArrayList 和 LinkedList 的实现原理和各自的特点。那接下来,我们就来聊聊 ArrayList 和 LinkedList 在新增元素时究竟谁快?
ArrayList 新增元素有两种情况,一种是直接将元素添加到数组末尾,一种是将元素插入到指定位置。
添加到数组末尾的源码(这部分前面讲 ArrayList 的时候讲过了,这里再温故一下):
很简单,先判断是否需要扩容,然后直接通过索引将元素添加到末尾。
插入到指定位置的源码:
先检查插入的位置是否在合理的范围之内,然后判断是否需要扩容,再把该位置以后的元素复制到新添加元素的位置之后,最后通过索引将元素添加到指定的位置。
LinkedList 新增元素也有两种情况,一种是直接将元素添加到队尾,一种是将元素插入到指定位置。
添加到队尾的源码:
先将队尾的节点 last 存放到临时变量 l 中,然后生成新的 Node 节点,并赋给 last,如果 l 为 null,说明是第一次添加,所以 first 为新的节点;否则将新的节点赋给之前 last 的 next。
插入到指定位置的源码:
先检查插入的位置是否在合理的范围之内,然后判断插入的位置是否是队尾,如果是,添加到队尾;否则执行 方法。
在执行 方法之前,会调用 方法查找指定位置上的元素,这一步是需要遍历 LinkedList 的。如果插入的位置靠前前半段,就从队头开始往后找;否则从队尾往前找。也就是说,如果插入的位置越靠近 LinkedList 的中间位置,遍历所花费的时间就越多。
找到指定位置上的元素(参数succ)之后,就开始执行 方法,先将 succ 的前一个节点(prev)存放到临时变量 pred 中,然后生成新的 Node 节点(newNode),并将 succ 的前一个节点变更为 newNode,如果 pred 为 null,说明插入的是队头,所以 first 为新节点;否则将 pred 的后一个节点变更为 newNode。
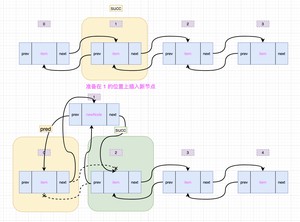
经过源码分析以后,你是不是在想:“好像 ArrayList 在新增元素的时候效率并不一定比 LinkedList 低啊!”
当两者的起始长度是一样的情况下:
- 如果是从集合的头部新增元素,ArrayList 花费的时间应该比 LinkedList 多,因为需要对头部以后的元素进行复制。
我们来测试一下:
num 为 10000,代码实测后的时间如下所示:
此时,ArrayList 花费的时间比 LinkedList 要多很多。
- 如果是从集合的中间位置新增元素,ArrayList 花费的时间搞不好要比 LinkedList 少,因为 LinkedList 需要遍历。
来看测试代码。
num 为 10000,代码实测后的时间如下所示:
ArrayList 花费的时间比 LinkedList 要少很多很多。
- 如果是从集合的尾部新增元素,ArrayList 花费的时间应该比 LinkedList 少,因为数组是一段连续的内存空间,也不需要复制数组;而链表需要创建新的对象,前后引用也要重新排列。
来看测试代码:
num 为 10000,代码实测后的时间如下所示:
ArrayList 花费的时间比 LinkedList 要少一些。
这样的结论和预期的是不是不太相符?ArrayList 在添加元素的时候如果不涉及到扩容,性能在两种情况下(中间位置新增元素、尾部新增元素)比 LinkedList 好很多,只有头部新增元素的时候比 LinkedList 差,因为数组复制的原因。
当然了,如果涉及到数组扩容的话,ArrayList 的性能就没那么可观了,因为扩容的时候也要复制数组。
ArrayList 删除元素的时候,有两种方式,一种是直接删除元素(),需要直先遍历数组,找到元素对应的索引;一种是按照索引删除元素()。
来看一下源码(其实前面也讲过了,这里温习一下):
本质上讲,两个方法是一样的,它们最后调用的都是 方法。
从源码可以看得出,只要删除的不是最后一个元素,都需要重新移动数组。删除的元素位置越靠前,代价就越大。
LinkedList 删除元素的时候,有四种常用的方式:
- ,删除指定位置上的元素
先检查索引,再调用 方法( 前后半段遍历,和新增元素操作一样)找到节点 Node,然后调用 解除节点的前后引用,同时更新前节点的后引用和后节点的前引用:
- ,直接删除元素
也是先前后半段遍历,找到要删除的元素后调用 。
- ,删除第一个节点
删除第一个节点就不需要遍历了,只需要把第二个节点更新为第一个节点即可。
- ,删除最后一个节点
删除最后一个节点和删除第一个节点类似,只需要把倒数第二个节点更新为最后一个节点即可。
可以看得出,LinkedList 在删除比较靠前和比较靠后的元素时,非常高效,但如果删除的是中间位置的元素,效率就比较低了。
这里就不再做代码测试了,感兴趣的话可以自己试试,结果和新增元素保持一致:
- 从集合头部删除元素时,ArrayList 花费的时间比 LinkedList 多很多;
- 从集合中间位置删除元素时,ArrayList 花费的时间比 LinkedList 少很多;
- 从集合尾部删除元素时,ArrayList 花费的时间比 LinkedList 少一点。
我本地的统计结果如下所示,可以作为参考:
遍历 ArrayList 找到某个元素的话,通常有两种形式:
- ,根据索引找元素
由于 ArrayList 是由数组实现的,所以根据索引找元素非常的快,一步到位。
- ,根据元素找索引
根据元素找索引的话,就需要遍历整个数组了,从头到尾依次找。
遍历 LinkedList 找到某个元素的话,通常也有两种形式:
- ,找指定位置上的元素
既然需要调用 方法,就意味着需要前后半段遍历了。
- ,找元素所在的位置
需要遍历整个链表,和 ArrayList 的 类似。
那在我们对集合遍历的时候,通常有两种做法,一种是使用 for 循环,一种是使用迭代器(Iterator)。
如果使用的是 for 循环,可想而知 LinkedList 在 get 的时候性能会非常差,因为每一次外层的 for 循环,都要执行一次 方法进行前后半段的遍历。
那如果使用的是迭代器呢?
迭代器只会调用一次 方法,在执行 的时候:先调用 AbstractSequentialList 类的 方法,再调用 AbstractList 类的 方法,再调用 LinkedList 类的 方法,如下图所示。
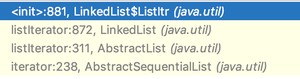
最后返回的是 LinkedList 类的内部私有类 ListItr 对象:
执行 ListItr 的构造方法时调用了一次 方法,返回第一个节点。在此之后,迭代器就执行 判断有没有下一个,执行 方法下一个节点。
由此,可以得出这样的结论:遍历 LinkedList 的时候,千万不要使用 for 循环,要使用迭代器。
也就是说,for 循环遍历的时候,ArrayList 花费的时间远小于 LinkedList;迭代器遍历的时候,两者性能差不多。
当需要频繁随机访问元素的时候,例如读取大量数据并进行处理或者需要对数据进行排序或查找的场景,可以使用 ArrayList。例如一个学生管理系统,需要对学生列表进行排序或查找操作,可以使用 ArrayList 存储学生信息,以便快速访问和处理。
当需要频繁插入和删除元素的时候,例如实现队列或栈,或者需要在中间插入或删除元素的场景,可以使用 LinkedList。例如一个实时聊天系统,需要实现一个消息队列,可以使用 LinkedList 存储消息,以便快速插入和删除消息。
在一些特殊场景下,可能需要同时支持随机访问和插入/删除操作。例如一个在线游戏系统,需要实现一个玩家列表,需要支持快速查找和遍历玩家,同时也需要支持玩家的加入和离开。在这种情况下,可以使用 LinkedList 和 ArrayList 的组合,例如使用 LinkedList 存储玩家,以便快速插入和删除玩家,同时使用 ArrayList 存储玩家列表,以便快速查找和遍历玩家。
“好了,三妹,关于 LinkedList 和 ArrayList 的差别,我们就先聊到这,你也不用太去扣细节,直到其中的差别就好了。”
“好的,二哥。”
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括Java基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 10000+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

“二哥,为什么要设计泛型啊?”三妹开门见山地问。
“三妹啊,听哥慢慢给你讲啊。”我说。
Java 在 1.5 时增加了泛型机制,据说专家们为此花费了 5 年左右的时间(听起来是相当不容易)。有了泛型之后,尤其是对集合类的使用,就变得更规范了。
看下面这段简单的代码。
“三妹,你能想象到在没有泛型之前该怎么办吗?”
“嗯,想不到,还是二哥你说吧。”
嗯,我们可以使用 Object 数组来设计 类。
然后,我们向 中存取数据。
“三妹,你有没有发现这两个问题?”
- Arraylist 可以存放任何类型的数据(既可以存字符串,也可以混入日期),因为所有类都继承自 Object 类。
- 从 Arraylist 取出数据的时候需要强制类型转换,因为编译器并不能确定你取的是字符串还是日期。
“嗯嗯,是的呢。”三妹说。
对比一下,你就能明显地感受到泛型的优秀之处:使用类型参数解决了元素的不确定性——参数类型为 String 的集合中是不允许存放其他类型元素的,取出数据的时候也不需要强制类型转换了。
“二哥,那怎么才能设计一个泛型呢?”
“三妹啊,你一个小白只要会用泛型就行了,还想设计泛型啊?!不过,既然你想了解,哥义不容辞。”
首先,我们来按照泛型的标准重新设计一下 类。
一个泛型类就是具有一个或多个类型变量的类。Arraylist 类引入的类型变量为 E(Element,元素的首字母),使用尖括号 括起来,放在类名的后面。
然后,我们可以用具体的类型(比如字符串)替换类型变量来实例化泛型类。
Date 类型也可以的。
其次,我们还可以在一个非泛型的类(或者泛型类)中定义泛型方法。
不过,说实话,泛型方法的定义看起来略显晦涩。来一副图吧(注意:方法返回类型和方法参数类型至少需要一个)。

现在,我们来调用一下泛型方法。
然后,我们再来说说泛型变量的限定符 。
在解释这个限定符之前,我们假设有三个类,它们之间的定义是这样的。
我们使用限定符 来重新设计一下 类。
当我们向 中添加 元素的时候,编译器会提示错误: 只允许添加 及其子类 对象,不允许添加其父类 。
也就是说,限定符 可以缩小泛型的类型范围。
“哦,明白了。”三妹若有所思的点点头,“二哥,听说虚拟机没有泛型?”
“三妹,你功课做得可以啊。哥可以肯定地回答你,虚拟机是没有泛型的。”
“怎么确定虚拟机有没有泛型呢?”三妹问。
“只要我们把泛型类的字节码进行反编译就看到了!”用反编译工具(我写这篇文章的时候用的是 jad,你也可以用其他的工具)将 class 文件反编译后,我说,“三妹,你看。”
类型变量 消失了,取而代之的是 Object !
“既然如此,那如果泛型类使用了限定符 ,结果会怎么样呢?”三妹这个问题问的很巧妙。
来看这段代码。
反编译后的结果如下。
“你看,类型变量 不见了,E 被替换成了 ”,我说,“通过以上两个例子说明,Java 虚拟机会将泛型的类型变量擦除,并替换为限定类型(没有限定的话,就用 )”
“二哥,类型擦除会有什么问题吗?”三妹又问了一个很有水平的问题。
“三妹啊,你还别说,类型擦除真的会有一些问题。”我说,“来看一下这段代码。”
在浅层的意识上,我们会想当然地认为 和 是两种不同的类型,因为 String 和 Date 是不同的类。
但由于类型擦除的原因,以上代码是不会通过编译的——编译器会提示一个错误(这正是类型擦除引发的那些“问题”):
大致的意思就是,这两个方法的参数类型在擦除后是相同的。
也就是说, 和 是同一种参数类型的方法,不能同时存在。类型变量 和 在擦除后会自动消失,method 方法的实际参数是 。
有句俗话叫做:“百闻不如一见”,但即使见到了也未必为真——泛型的擦除问题就可以很好地佐证这个观点。
“哦,明白了。二哥,听说泛型还有通配符?”
“三妹啊,哥突然觉得你很适合作一枚可爱的程序媛啊!你这预习的功课做得可真到家啊,连通配符都知道!”
通配符使用英文的问号来表示。在我们创建一个泛型对象时,可以使用关键字 限定子类,也可以使用关键字 限定父类。
我们来看下面这段代码。
1)新增 方法,判断元素在 中的位置。注意参数为 而不是泛型 。
2)新增 方法,判断元素是否在 中。注意参数为 而不是泛型 。
3)新增 方法,方便对 进行打印。
4)新增 方法,方便对 元素的更改。
因为泛型擦除的原因, 这样的语句是无法通过编译的,尽管 Wangxiaoer 是 Wanger 的子类。但如果我们确实需要这种 “向上转型” 的关系,该怎么办呢?这时候就需要通配符来发挥作用了。
利用 形式的通配符,可以实现泛型的向上转型,来看例子。
list2 的类型是 ,翻译一下就是,list2 是一个 ,其类型是 及其子类。
注意,“关键”来了!list2 并不允许通过 方法向其添加 或者 的对象,唯一例外的是 。
“那就奇了怪了,既然不让存放元素,那要 这样的 list2 有什么用呢?”三妹好奇地问。
虽然不能通过 方法往 list2 中添加元素,但可以给它赋值。
语句把 list 的值赋予了 list2,此时 。由于 list2 不允许往其添加其他元素,所以此时它是安全的——我们可以从容地对 list2 进行 、 和 。想一想,如果可以向 list2 添加元素的话,这 3 个方法反而变得不太安全,它们的值可能就会变。
利用 形式的通配符,可以向 Arraylist 中存入父类是 的元素,来看例子。
需要注意的是,无法从 这样类型的 list3 中取出数据。
好了,三妹,关于泛型,我们再来做一个简单的总结。
在 Java 中,泛型是一种强类型约束机制,可以在编译期间检查类型安全性,并且可以提高代码的复用性和可读性。
泛型的本质是参数化类型,也就是说,在定义类、接口或方法时,可以使用一个或多个类型参数来表示参数化类型。
例如这样可以定义一个泛型类。
在这个例子中, 表示类型参数,可以在类中任何需要使用类型的地方使用 T 代替具体的类型。通过使用泛型,我们可以创建一个可以存储任何类型对象的盒子。
泛型在实际开发中的应用非常广泛,例如集合框架中的 List、Set、Map 等容器类,以及并发框架中的 Future、Callable 等工具类都使用了泛型。
在 Java 的泛型机制中,有两个重要的概念:类型擦除和通配符。
泛型在编译时会将泛型类型擦除,将泛型类型替换成 Object 类型。这是为了向后兼容,避免对原有的 Java 代码造成影响。
例如,对于下面的代码:
在编译时,Java 编译器会将泛型类型 替换成 ,将 get 方法的返回值类型 Integer 替换成 Object,生成的字节码与下面的代码等价:
Java 泛型只在编译时起作用,运行时并不会保留泛型类型信息。
通配符用于表示某种未知的类型,例如 表示一个可以存储任何类型对象的 List,但是不能对其中的元素进行添加操作。通配符可以用来解决类型不确定的情况,例如在方法参数或返回值中使用。
使用通配符可以使方法更加通用,同时保证类型安全。
例如,定义一个泛型方法:
这个方法可以接受任意类型的 List,例如 、 等等。
泛型还提供了上限通配符 ,表示通配符只能接受 T 或 T 的子类。使用上限通配符可以提高程序的类型安全性。
例如,定义一个方法,只接受 Number 及其子类的 List:
这个方法可以接受 、 等等。
下限通配符(Lower Bounded Wildcards)用 super 关键字来声明,其语法形式为 ,其中 T 表示类型参数。它表示的是该类型参数必须是某个指定类的超类(包括该类本身)。
当我们需要往一个泛型集合中添加元素时,如果使用的是上限通配符,集合中的元素类型可能会被限制,从而无法添加某些类型的元素。但是,如果我们使用下限通配符,可以将指定类型的子类型添加到集合中,保证了元素的完整性。
举个例子,假设有一个类 Animal,以及两个子类 Dog 和 Cat。现在我们有一个 集合,它的类型参数必须是 Dog 或其父类类型。我们可以向该集合中添加 Dog 类型的元素,也可以添加它的子类。但是,不能向其中添加 Cat 类型的元素,因为 Cat 不是 Dog 的子类。
下面是一个使用下限通配符的示例:
需要注意的是,虽然使用下限通配符可以添加某些子类型元素,但是在读取元素时,我们只能确保其是 Object 类型的,无法确保其是指定类型或其父类型。因此,在读取元素时需要进行类型转换,如下所示:
总的来说,Java 的泛型机制是一种非常强大的类型约束机制,可以在编译时检查类型安全性,并提高代码的复用性和可读性。但是,在使用泛型时也需要注意类型擦除和通配符等问题,以确保代码的正确性。
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括Java基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 10000+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

PS: 这篇同样来换一个风格,一起来欣赏。
那天,小二去海康威视面试,面试官老王一上来就甩给了他一道面试题:请问 Iterator与Iterable有什么区别?
小二表示很开心,因为他3 天前刚好在《二哥的Java进阶之路》上读过这篇文章,所以回答得胸有成竹。
以下↓是小二当时读过的文章内容,他印象深刻。
在 Java 中,我们对 List 进行遍历的时候,主要有这么三种方式。
第一种:for 循环。
第二种:迭代器。
第三种:for-each。
第一种我们略过,第二种用的是 Iterator,第三种看起来是 for-each,其实背后也是 Iterator,看一下反编译后的代码(如下所示)就明白了。
for-each 只不过是个语法糖,让我们开发者在遍历 List 的时候可以写更少的代码,更简洁明了。
Iterator 是个接口,JDK 1.2 的时候就有了,用来改进 Enumeration 接口:
- 允许删除元素(增加了 remove 方法)
- 优化了方法名(Enumeration 中是 hasMoreElements 和 nextElement,不简洁)
来看一下 Iterator 的源码:
JDK 1.8 时,Iterable 接口中新增了 forEach 方法。该方法接受一个 Consumer 对象作为参数,用于对集合中的每个元素执行指定的操作。该方法的实现方式是使用 for-each 循环遍历集合中的元素,对于每个元素,调用 Consumer 对象的 accept 方法执行指定的操作。
该方法实现时首先会对 action 参数进行非空检查,如果为 null 则抛出 NullPointerException 异常。然后使用 for-each 循环遍历集合中的元素,并对每个元素调用 action.accept(t) 方法执行指定的操作。由于 Iterable 接口是 Java 集合框架中所有集合类型的基本接口,因此该方法可以被所有实现了 Iterable 接口的集合类型使用。
它对 Iterable 的每个元素执行给定操作,具体指定的操作需要自己写Consumer接口通过accept方法回调出来。
写得更浅显易懂点,就是:
如果我们仔细观察ArrayList 或者 LinkedList 的“户口本”就会发现,并没有直接找到 Iterator 的影子。
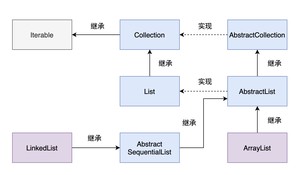
反而找到了 Iterable!
也就是说,List 的关系图谱中并没有直接使用 Iterator,而是使用 Iterable 做了过渡。
回头再来看一下第二种遍历 List 的方式。
发现刚好呼应上了。拿 ArrayList 来说吧,它重写了 Iterable 接口的 iterator 方法:
返回的对象 Itr 是个内部类,实现了 Iterator 接口,并且按照自己的方式重写了 hasNext、next、remove 等方法。
那可能有些小伙伴会问:为什么不直接将 Iterator 中的核心方法 hasNext、next 放到 Iterable 接口中呢?直接像下面这样使用不是更方便?
从英文单词的后缀语法上来看,(Iterable)able 表示这个 List 是支持迭代的,而 (Iterator)tor 表示这个 List 是如何迭代的。
支持迭代与具体怎么迭代显然不能混在一起,否则就乱的一笔。还是各司其职的好。
想一下,如果把 Iterator 和 Iterable 合并,for-each 这种遍历 List 的方式是不是就不好办了?
原则上,只要一个 List 实现了 Iterable 接口,那么它就可以使用 for-each 这种方式来遍历,那具体该怎么遍历,还是要看它自己是怎么实现 Iterator 接口的。
Map 就没办法直接使用 for-each,因为 Map 没有实现 Iterable 接口,只有通过 、、 这种返回一个 Collection 的方式才能 使用 for-each。
如果我们仔细研究 LinkedList 的源码就会发现,LinkedList 并没有直接重写 Iterable 接口的 iterator 方法,而是由它的父类 AbstractSequentialList 来完成。
LinkedList 重写了 listIterator 方法:
这里我们发现了一个新的迭代器 ListIterator,它继承了 Iterator 接口,在遍历List 时可以从任意下标开始遍历,而且支持双向遍历。
我们知道,集合(Collection)不仅有 List,还有 Set,那 Iterator 不仅支持 List,还支持 Set,但 ListIterator 就只支持 List。
那可能有些小伙伴会问:为什么不直接让 List 实现 Iterator 接口,而是要用内部类来实现呢?
这是因为有些 List 可能会有多种遍历方式,比如说 LinkedList,除了支持正序的遍历方式,还支持逆序的遍历方式——DescendingIterator:
可以看得到,DescendingIterator 刚好利用了 ListIterator 向前遍历的方式。可以通过以下的方式来使用:
好了,关于Iterator与Iterable我们就先聊这么多,总结两点:
- 学会深入思考,一点点抽丝剥茧,多想想为什么这样实现,很多问题没有自己想象中的那么复杂。
- 遇到疑惑不放弃,这是提升自己最好的机会,遇到某个疑难的点,解决的过程中会挖掘出很多相关的东西。
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括Java基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 10000+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

这篇文章同样采用小二去面试的形式,给大家换个胃口。
那天,小二去阿里面试,面试官老王一上来就甩给了他一道面试题:为什么阿里的 Java 开发手册里会强制不要在 foreach 里进行元素的删除操作?

小二听完这句话就乐了。为什么呢?因为一天前他刚在《二哥的Java进阶之路》上看到过这道题的答案。
以下是整篇文章的内容。
为了镇楼,先搬一段英文来解释一下 fail-fast。
In systems design, a fail-fast system is one which immediately reports at its interface any condition that is likely to indicate a failure. Fail-fast systems are usually designed to stop normal operation rather than attempt to continue a possibly flawed process. Such designs often check the system's state at several points in an operation, so any failures can be detected early. The responsibility of a fail-fast module is detecting errors, then letting the next-highest level of the system handle them.
这段话的大致意思就是,fail-fast 是一种通用的系统设计思想,一旦检测到可能会发生错误,就立马抛出异常,程序将不再往下执行。
一旦检测到 wanger 为 null,就立马抛出异常,让调用者来决定这种情况下该怎么处理,下一步 就不会执行了——避免更严重的错误出现。
很多时候,我们会把 fail-fast 归类为 Java 集合框架的一种错误检测机制,但其实 fail-fast 并不是 Java 集合框架特有的机制。
之所以我们把 fail-fast 放在集合框架篇里介绍,是因为问题比较容易再现。
这段代码看起来没有任何问题,但运行起来就报错了。

根据错误的堆栈信息,我们可以定位到 ArrayList 的第 901 行代码。
也就是说,remove 的时候触发执行了 方法,该方法对 modCount 和 expectedModCount 进行了比较,发现两者不等,就抛出了 异常。
为什么会执行 方法呢?
是因为 for-each 本质上是个语法糖,底层是通过迭代器 Iterator 配合 while 循环实现的,来看一下反编译后的字节码。
来看一下 ArrayList 的 iterator 方法吧:
内部类 Itr 实现了 Iterator 接口,这是 Itr 的源码。
也就是说 的时候 expectedModCount 被赋值为 modCount,而 modCount 是 ArrayList 中的一个计数器,用于记录 ArrayList 对象被修改的次数。ArrayList 的修改操作包括添加、删除、设置元素值等。每次对 ArrayList 进行修改操作时,modCount 的值会自增 1。
在迭代 ArrayList 时,如果迭代过程中发现 modCount 的值与迭代器的 expectedModCount 不一致,则说明 ArrayList 已被修改过,此时会抛出 ConcurrentModificationException 异常。这种机制可以保证迭代器在遍历 ArrayList 时,不会遗漏或重复元素,同时也可以在多线程环境下检测到并发修改问题。
我们来继续定位之前报错的错误堆栈。这是之前的代码。
由于 list 此前执行了 3 次 add 方法。
- add 方法调用 ensureCapacityInternal 方法
- ensureCapacityInternal 方法调用 ensureExplicitCapacity 方法
- ensureExplicitCapacity 方法中会执行
所以 modCount 的值在经过三次 add 后为 3,于是 后 expectedModCount 的值也为 3(回到前面去看一下 Itr 的源码)。
接着来执行 for-each 的循环遍历。
执行第一次循环时,发现“沉默王二”等于 str,于是执行 。
- remove 方法调用 fastRemove 方法
- fastRemove 方法中会执行
modCount 的值变成了 4。
第二次遍历时,会执行 Itr 的 next 方法(),next 方法就会调用 方法。
此时 expectedModCount 为 3,modCount 为 4,就只好抛出 ConcurrentModificationException 异常了。
那其实在阿里巴巴的 Java 开发手册里也提到了,不要在 for-each 循环里进行元素的 remove/add 操作。remove 元素请使用 Iterator 方式。

那原因其实就是我们上面分析的这些,出于 fail-fast 保护机制。
break 后循环就不再遍历了,意味着 Iterator 的 next 方法不再执行了,也就意味着 方法不再执行了,所以异常也就不会抛出了。
但是呢,当 List 中有重复元素要删除的时候,break 就不合适了。
for 循环虽然可以避开 fail-fast 保护机制,也就说 remove 元素后不再抛出异常;但是呢,这段程序在原则上是有问题的。为什么呢?
第一次循环的时候,i 为 0, 为 3,当执行完 remove 方法后,i 为 1, 却变成了 2,因为 list 的大小在 remove 后发生了变化,也就意味着“沉默王三”这个元素被跳过了。能明白吗?
remove 之前 为“沉默王三”;但 remove 之后 变成了“一个文章真特么有趣的程序员”,而 变成了“沉默王三”。
为什么使用 Iterator 的 remove 方法就可以避开 fail-fast 保护机制呢?看一下 remove 的源码就明白了。
删除完会执行 ,保证了 expectedModCount 与 modCount 的同步。
为什么不能在foreach里执行删除操作?
因为 foreach 循环是基于迭代器实现的,而迭代器在遍历集合时会维护一个 expectedModCount 属性来记录集合被修改的次数。如果在 foreach 循环中执行删除操作会导致 expectedModCount 属性值与实际的 modCount 属性值不一致,从而导致迭代器的 hasNext() 和 next() 方法抛出 ConcurrentModificationException 异常。
为了避免这种情况,应该使用迭代器的 remove() 方法来删除元素,该方法会在删除元素后更新迭代器状态,确保循环的正确性。如果需要在循环中删除元素,应该使用迭代器的 remove() 方法,而不是集合自身的 remove() 方法。
就像这样。
除此之外,我们还可以采用 Stream 流的filter() 方法来过滤集合中的元素,然后再通过 collect() 方法将过滤后的元素收集到一个新的集合中。
好了,关于这个问题,就聊到这里吧,希望能帮助到你。
GitHub 上标星 10000+ 的开源知识库《二哥的 Java 进阶之路》第一版 PDF 终于来了!包括Java基础语法、数组&字符串、OOP、集合框架、Java IO、异常处理、Java 新特性、网络编程、NIO、并发编程、JVM等等,共计 32 万余字,500+张手绘图,可以说是通俗易懂、风趣幽默……详情戳:太赞了,GitHub 上标星 10000+ 的 Java 教程
微信搜 沉默王二 或扫描下方二维码关注二哥的原创公众号沉默王二,回复 222 即可免费领取。

版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/3660.html
