写在前面,网上的一些教程实在一言难尽,,,当然我这篇也是(狗头)。所以我打算写一篇自己可以理解的树状数组维护区间最值,以最大值举例。需要树状数组维护区间和的相关知识,好,进入正题。
如果我们求维护区间和,我们是这么写的:
那我们维护区间最大值,能不能这么写呢?试着写一下:
好像很正确的样子,因为c[i]由k组成,c[i]又直接关系到c[i+lowbit(i)],这么一路改过去就好了。
但是有一个例外,设数组为arr,如果恰巧c[i]=arr[i],即c[i]管辖的区间的最大值就是arr[i],且恰巧区间内其他值也没有等于arr[i]的,而咱们还恰好更改了arr[i],而且这个值k恰巧小于原来的arr[i],那么想想看,arr[i]变了之后c[i]就不可能等于原arr[i],但是add函数仍让我们c[i]等于原arr[i]。那肯定错误了。再极端一下,原arr[i]就是原数组的最大值,那岂不错的更离谱了!??
这只是一个情况,更多细节各位可以自己捋清楚。
那要怎么办?
(个人不会画图,用的是区间和那个,看图就行,不用在意其它文字,图片出自 https://blog.csdn.net/bestsort/article/details/)
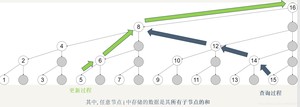
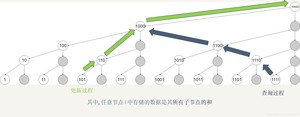
下面是奇丑无比的代码:
这样的时间复杂度为
时间复杂度为
其实这么写单点更新也是可以的:
不过对应特殊情况,比如求最长上升子序列等问题,因为对于dp问题,我们每次要求选择最优,比如,连续上升子序列问题中,若k小于等于arr[i],那么我们就不用替换,就可以避免之前说的问题。这样我们可以用时间复杂度仅为O(logn)的函数完成单点更新。
个人片面的理解,如有疏漏,欢迎指出。
版权声明:
本文来源网络,所有图片文章版权属于原作者,如有侵权,联系删除。
本文网址:https://www.mushiming.com/mjsbk/4353.html
