数学建模预测模型有哪些



预测和分类本质上没啥区别，都是找到一个合适的函数做预测/分类。所以能做预测的模型多半可以做分类。

条件： 大量数据（题目给出大量数据时，就算题中没有要求进行数据清洗也要进行！！！主要处理异常值和缺失值，处理时候也不要单纯的进行删除，会让老师觉得你有点low）
注意：

1. 交代清楚 input 和 output 都是什么
2. 迭代次数，学习率等超参数写清楚，最好也写清楚是怎么调整的参数
3. 神经网络有多少层 每层多少个结点 为什么选择这样设置
4. 由于神经网络没有数学模型，所以评价标准很重要。准确率，损失函数，稳定性评价指标最好都有，选择什么样的计算公式要写清楚

理论性不强，没法论证，能不用就不用，数据量非常少的时候可以考虑

拟合是给定了空间中的一些点，找到一个已知形式未知参数的连续曲面来最大限度地逼近这些点；而插值是找到一个 (或几个分片光滑的)连续曲面来穿过这些点。

要求数据是等间距的，与马尔科夫模型是互补的
应用： 求解季节模型

序列之间前后传递比较少的，数据和数据之间随机性比较强（比如今明天的气温没有直接联系，只能从趋势判断后天温度是多少）

找不到数据之间的关系，但是能找到变化量之间的关系的时候用

分析一个因变量和很多个自变量的联系
缺点： 要求变量之间的相关性需要比较小，样本的个数需要大于三倍自变量个数，容易欠拟合，一般准确度不太高，因变量Y为定类数据
在有很多因变量的时候可以用主成分分析或者聚类分析 减少自变量
应用： 最经典的是：葡萄酒规划的问题上（好多因变量共同评价葡萄酒的品质）
在逻辑回归结果很差的情况下，决策树一般会比较好解决，适合少量样本多维特征情况，完美解决欠拟合。或者可以考虑用降维方法之后再用逻辑回归。

缺点：因变量Y（被解释变量）一定是定量数据，分类问题必须线性可分

• 数据缺失用插值，最好不用插值做预测
• 拟合是最简单的预测（预测也相对准确）
• 神经网络预测最缺率最高
• 灰色预测应用相对简单，但是学起来麻烦
• 所以缺失就用插值，其他的就用神经网络，神经网络运算量太大的时候就用拟合

人口预测，水资源污染预测，病毒蔓延预测，经济发展情况预测…

参考文章：数学建模题型之分类

主要思想：找到一个超平面，使得它能够尽可能多地将两类数据点正确分开，同时使分开的两类数据点距离分类面最远
优点：适用于高维数据；能够处理非线性特征之间的相互作用；占用内存小，泛化能力好。
缺点：当观测样本很多时，效率并不是很高；有时候很难找到一个合适的核函数，对参数和核函数的选择比较敏感，原始的SVM只比较擅长处理二分类问题；这里也是个二分类问题 我觉得也可以进行svm尝试

2.3.1 基于划分的聚类k-means

优点： 收敛速度快，准确度高，对数据没有假设，对outlier不敏感；可用于非线性分类；
缺点： 对K值的选取不好把握；对于不是凸的数据集比较难收敛；采用迭代方法，得到的结果只是局部最优；对噪音和异常点比较的敏感；计算量大； 样本不平衡问题（即有些类别的样本数量很多，而其它样本的数量很少）；
FCM聚类与K-means聚类的分析比较

2.3.2 基于层次的聚类

优点： 可解释性好（如当需要创建一种分类法时）；还有些研究表明这些算法能产生高质量的聚类，也会应用在上面说的先取K比较大的K-means后的合并阶段；还有对于K-means不能解决的非球形族就可以解决了。
缺点： 时间复杂度高，贪心算法的缺点，一步错步步错

2.3.3 基于模型的聚类 SOM

优点： 对”类“的划分以概率形式表现，每一类的特征也可以用参数来表达。
缺点： 执行效率不高，特别是分布数量很多并且数据量很少的时候。
Matlab代码实现SOM(自组织映射)算法

2.3.4 FCM（模糊聚类）

优点： 算法对于满足正态分布的数据聚类效果会很好，另外，算法对孤立点是敏感的。
缺点： 由于不能确保FCM收敛于一个最优解，算法的性能依赖于初始聚类中心。比k-means速度慢
解决缺点的办法：

• 每次用不同的初始聚类中心启动该算法，多次运行FCM
• 用另外的快速算法确定初始聚类中心
  FCM算法Matlab实现

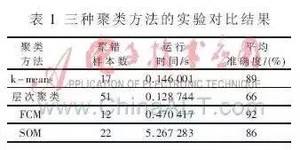
四种聚类算法比较

• k-means聚类算法的初始点选择不稳定，是随机选取的，这就引起聚类结果的不稳定，本实验中虽是经过多次实验取的平均值，但是具体初始点的选择方法还需进一步研究；
• 层次聚类虽然不需要确定分类数，但是一旦一个分裂或者合并被执行，就不能修正，聚类质量受限制；
• FCM对初始聚类中心敏感，需要人为确定聚类数，容易陷入局部最优 解；
• SOM与实际大脑处理有很强的理论联系。但是处理时间较长，需要进一步研究使其适应大型数据库。
  3.

总结：

对于建模最好先用一种聚类得到中心点，然后用 FCM

2.3.5 spss聚类分析：

https://blog.csdn.net/LuYi_WeiLin/article/details/

使用主成分分析法进行降维时要求：

1. 数据线性相关
2. 所有变量是连续型变量
3. 尽量服从正态分布

通常用来分析两个特征之间的关系，计算量比较大，当题目中问哪个和这个特征更相关时可以考虑。也可以用来降维，降相关性更大的作为特征输入。或者用来筛选不相关特征，以便可以适应效率更高的逻辑回归模型。

主要用于图像分类

数据是分类变量或者连续变量中的一种，不能混用，否则结果后悔很差（进行预测的时候可以先用别的算法判断对模型有影响的指标—比如决策树，再进行训练）
e.g.连续变量：评分，年龄…
分类变量：性别（类似男用0女用1代替），工作（给几类工作用0-7分别表示之类的）

优点： 计算量简单，可解释性强，比较适合处理有缺失属性值的样本，能够处理不相关的特征；
缺点： 容易过拟合（后续出现了随机森林，减小了过拟合现象）；

参考文章：数学建模优化及算法总结

目标规划

线性规划

非线性规划

整数规划

动态规划

3.4.1 遗传算法

3.4.2 模拟退火算法

3.4.3 禁忌搜索算法

3.4.4 蚁群算法

• 在假设成一种函数形式找到最优解之后，再与其他函数形式结果进行比较的时候，可以先将其他函数与心在得到的最优解进行拟合，这样可以节省从头开始优化的计算量（因为已经优化过一次了，准确的曲线应该就在这条线附近）
• 视频跳转： 35分钟左右讲的

参考链接：1、2
基本思想： 主成分分析的主要目的是希望用较少的变量去解释原来资料中的大部分变异，通常是选出比原始 变量个数少，能解释大部分资料中的变异的几个新变量，即所谓主成分。
计算步骤：

• 对原始数据进行标准化处理
• 计算相关系数R
• 计算特征值和特征向量
• 选择 p (p <= m)个主成分，计算综合评价值
• matlab实现主成分分析的pcacov( )函数
  缺点
• 要求有大量数据,数据量少就难以找出统计规律;
• 要求样本服从某个典型的概率分布，要求各因素数据与系统特征数据之间呈线性关系且各因素之间彼此无关,这种要求往往难以满足;
• 计算量大,一般要靠计算机帮助;
• 可能出现量化结果与定性分析结果不符的现象，导致系统的关系和规律遭到歪曲和颠倒。

参考博客：1、 2
灰色关联分析方法，是根据因素之间发展趋势的相似或相异程度，亦即“灰色关联度”，作为衡量因素间关联程度的一种方法。曲线越接近,相应序列之间的关联度就越大,反之就越小。
优点：
样本量的多少和样本有无规律都同样适用
而且计算量小，十分方便
不会出现量化结果与定性分析结果不符的情况。

计算步骤
1.画统计图
2.确定分析数列

• 母序列（母指标）：能反映系统行为特征的数据序列，类似于因变量Y
• 子序列（子指标）：影响系统行为的因素组成的数据序列，类似于自变量X

参考博客：1

参考博客：点击跳转
一种通过样本数据确定评价指标权重的方法
原理： 指标的变异程度越小，所反映的现有信息量也越少，其对应的权值也越低。也就是说，熵权法是使用指标内部所包含的信息量，来确定该指标在所有指标之中的地位。
计算步骤：

• 对于输入矩阵，先进性正向化和标准化
• 计算第j项指标下第i个样本所占的比重，并将其看作信息熵计算中用到的概率
• 计算每个指标的信息熵，并计算信息效用值，归一化之后得到每个指标的熵权

缺点：
只从数据出发，不考虑问题的实际背景，确定权重时就可能出现与常识相悖的情况。

遇到一道题可以优先选用模糊综合评价算法，其他算法用来佐证模糊综合评价算法的结果

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/779.html