常见的模型评估指标有哪些



均方误差（Mean Square Error）简称MSE，公式如下：

其中y_i表示真实值，比如模型的真实，比如模型的label；“y_i尖”是预测值，如常用的y_pred。
MSE的范围：[0,+∞)，预测值和真实值完全吻合时，MSE=0，即完美模型（实际模型训练中，基本不会出现的啦！！！）；误差越大，MSE该值越大。
（目前没有时间学习latex公式啊，等我学会了，再更新下，重新敲啊，大家饶过我吧，哈哈）

均方根误差（Root Mean Square Error）简称RMSE，公式如下：

其实就是MSE开根号得到的，已经有MSE了，为啥还定义一个开根号版本（RMSE）呢？据解释说这样数量级上比较直观。
RMSE的范围：[0,+∞)，预测值和真实值完全吻合时，RMSE=0，即完美模型；误差越大，RMSE值越大。

平均绝对误差（Mean Absolute Error），简称MAE，公式如下：

MAE的范围：[0,+∞)，预测值和真实值完全吻合时，MAE=0，即完美模型；误差越大，MAE值越大。
MAE对极端值比较敏感，当没有MSE敏感。

平均绝对百分比误差（Mean Absolute Percentage Error），简称MAPE，公式如下：

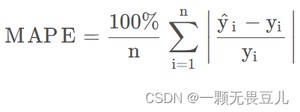
和MAE很像，就是MAE除了一个分母。
MAPE的范围：[0,+∞)，预测值和真实值完全吻合时，MAPE=0，即完美模型；误差越大，MAPE值越大。
注意：当真实值y_i中存在数据等于0时，该公式不可用，因分母不能为0

对称平均绝对百分比误差（Symmetric Mean Absolute Percentage Error）简称SMAPE，公式如下：

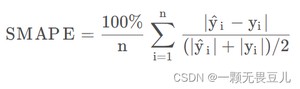
和MAE和MAPE都很像，首先，是在MAE的基础上除以了一个分母，其次，MAPE除以的分母不同罢了
注意：当真实值y_i中有数据为0，且预测值“y_i尖”中也有数据为0时，该公式不可用，存在分母为0问题。

均方对数误差（Mean Squared Log Error），简称MSLE，公式如下：

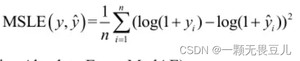
中位绝对误差（Median Absolute Error）简称MedAE，公式如下：

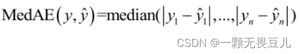
1.单个指标选用：

• 当看重真实值和预测值间的差的平方时，选用MSE或RMSE
• 当看重真实值和预测值间的绝对值误差时，选用MAE或MedAE，两者分别是误差的均值和中位数，MAE对极端值比较敏感
• 当看重真实值的数据中存在量级差，或不同样本的真实值存在量级差，而且更加关注真实值和预测值的百分比差异时，选用MAPE或SMAPE
• 当y具有随着x进行指数变动的趋势时，选用MSLE

2.多个指标搭配使用

• RMSE与MAE联合使用，可以看出样本误差的离散程度，若RMSE远大于MAE，则可以知道不同样本的误差差别很大
• MAE与MAPE，再结合“y八”（即y一横，y平均），可以估算不同数量级样例的拟合程度，若MAE远大于MAPE*（y平均），则可能是模型对真实值小的样本预测更准，此时就可以考虑为不同数量级的样本建立不同的模型。

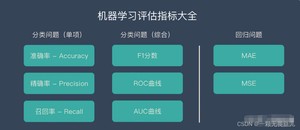
准确率（Accuracy）

准确率是指预测正确的结果占总样本的百分比，公式如下：
Acc=(TP+TN)/(TP+TN+FP+FN)
注意：当样本不平衡时，准确率不适合作为衡量指标，即样本不平衡时，准确率就会失效。如：一个总样本中，正样本占90%，负样本占10%，样本是严重不平衡的，此时我们只需要将全部样本预测为正样本就可得到90%的高准确率，但实际我们并没有很用心的分类，只是随便无脑一分而已。

精确率/查准率（Precision）

召回率/查全率（Recall）

F1分数（F1 score）

F1分数是精确率和召回率的博弈，公式如下。精确率和召回率是相互制约的关系，即当精确率过高，召回率就会偏小当召回率过高，精确率就会偏小，其关系如下图2.2，当然，我们希望我们的模型精确率越高越好，召回率越高越好，但两者是矛盾的，所以我们选取一个点，一个两者间的平衡作为F1分数。
F1 score=(2×Precision×Recall)/(Precision+Recall)

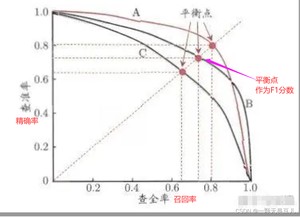
PR曲线

PR曲线是指以召回率为横坐标，精确率为纵坐标，如图2.2.1，AP是PR曲线与X轴、Y轴围成的面积，AP=1时的模型性能最好，AP越接近1越好，最小也得大于0.5。

ROC曲线

ROC曲线是指以假阳性率FPR为横坐标，真阳性率TPR为纵坐标，如图2.2.2。
假阳性率FPR：是指所有实际为负例的样本中，模型错误的预测为正例的样本比例，可以理解为所有阴性群体中被检测出来阳性的比率（误诊率），FPR越接近0越好，公式如下：
FPR=FP/(FP+TN)![在这里插入图片描述](https://img-blog.csdnimg.cn/direct/ad5df3f5166a4841ada39218b82bdce7.png

• (0,1)：即FPR=0, TPR=1，这意味着FN=0，并且FP=0。这是一个完美的分类器，它将所有的样本都正确分类。、
• (1,0)：即FPR=1，TPR=0，发现这是一个最糟糕的分类器，因为它成功避开了所有的正确答案
• (0,0)：即FPR=TPR=0，即FP=TP=0，可以发现该分类器预测所有的样本都为负样本。
• (1,1)：即FPR=TPR=1，即TN=FN=0，可以发现该分类器预测所有样本都为正样本。
• 虚线y=x：表示的是一个采用随机猜测策略的分类器的结果(FP = TN, TP = FN，这样FP+TP = TN + FN，即Y = N，也就是随机猜测了)，例如(0.5,0.5)，表示该分类器随机对于一半的样本猜测其为正样本，另外一半的样本为负样本。
  综上，ROC曲线越接近左上角，性能越好。

AUC曲线

AUC是指ROC曲线下的面积，用于衡量分类器性能，AUC越接近1，分类性能越好；AUC越接近0，分类性能越差。

• AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
• 0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
• AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
• AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

因为ROC曲线有个很好的特性：当测试集中的正负样本的分布变化的时候，ROC曲线能够保持不变。在实际的数据集中经常会出现类不平衡(class imbalance)现象，即负样本比正样本多很多(或者相反)，而且测试数据中的正负样本的分布也可能随着时间变化，用ROC作为衡量分类情况，更加稳定。下图是ROC曲线和Precision-Recall曲线的对比：

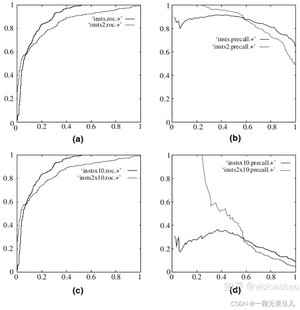
在上图中，(a)和©为ROC曲线，(b)和(d)为PR曲线。(a)和(b)展示的是分类其在原始测试集(正负样本分布平衡)的结果，©和(d)是将测试集中负样本的数量增加到原来的10倍后，分类器的结果。可以明显的看出，ROC曲线基本保持原貌，而PR曲线则变化较大。

MCC

马修斯相关系数（Matthews Correlation Coefficient），简称MCC，公式如下：

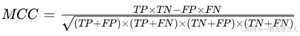
MCC的值范围：[-1,1]，其中，+1 表示预测准确率为 100%，即完美的预测，而值为 -1表示模型的预测完全与真实情况相反，即预测完全错误，0表示模型的性能等同于随机预测。
考虑了混淆矩阵中的真正例（TP）、真负例（TN）、假正例（FP）和假负例（FN）。
是一种用于评估二分类模型性能的指标。
当你需要评估模型的性能，特别是在数据集不平衡的情况下，MCC是一个比准确度（Accuracy）、精确度（Precision）或召回率（Recall）更全面的指标，因为它同时考虑了所有类别的预测性能。

PCC

皮尔逊相关系数（Pearson’s Correlation Coefficient），简称PCC，公式如下：

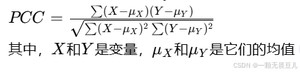
PCC值范围：[-1,1]，PCC为1时表示完全正相关，为-1时表示完全负相关，为0时表示没有线性相关性。
用于度量两个变量之间线性相关程度的统计量。
测量两个变量的协方差（联合变异性）与标准差（个体变异性）的比率。

平均绝对误差（Mean Absolute Error），简称MAE，公式如下：

MAE的范围：[0,+∞)，预测值和真实值完全吻合时，MAE=0，即完美模型；误差越大，MAE值越大。
MAE对极端值比较敏感。
下图是MAE函数的图像，其中真实值（目标值）是100，预测值范围为[-1000,1000]，Y轴代表MAE取值范围从[0,+∞），且损失在100处最小。

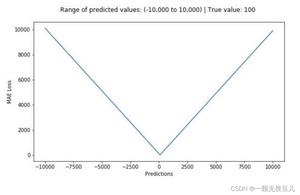
均方误差（Mean Square Error）简称MSE，公式如下：

其中y_i表示真实值，比如模型的真实，比如模型的label；“y_i尖”是预测值，如常用的y_pred。
MSE的范围：[0,+∞)，预测值和真实值完全吻合时，MSE=0，即完美模型（实际模型训练中，基本不会出现的啦！！！）；误差越大，MSE该值越大。
下图是MSE函数的图像，其中真实值（目标值）是100，预测值范围为[-1000,1000]，Y轴代表MSE取值范围从[0,+∞），且损失在100处最小。

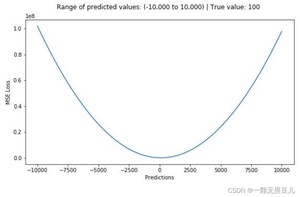
均方根误差（Root Mean Square Error）简称RMSE，公式如下：

其实就是MSE开根号得到的，已经有MSE了，为啥还定义一个开根号版本（RMSE）呢？据解释说这样数量级上比较直观。
RMSE的范围：[0,+∞)，预测值和真实值完全吻合时，RMSE=0，即完美模型；误差越大，RMSE值越大。

• MSE计算简便，但MAE对异常点具有更好的鲁棒性，RMSE是MSE的平方根，与MAE在同一量级
• MSE对误差取了平方（令e=真实值-预测值），因此若e>1，则MSE会进一步增大误差。如果数据中存在异常点，那么e值就会很大，而e则会远大于|e|。因此，相对于使用MAE计算损失，使用MSE的模型会赋予异常点更大的权重。
• 用RMSE计算损失的模型会以牺牲了其他样本的误差为代价，朝着减小异常点误差的方向更新，然而这就会降低模型的整体性能。如果训练数据被异常点所污染，那么MAE损失就更好用。
• MAE存在一个严重的问题（特别是对于神经网络）：更新的梯度始终相同，也就是说，即使对于很小的损失值，梯度也很大，这样不利于模型的学习。为了解决这个缺陷，可以使用变化的学习率，在损失接近最小值时降低学习率。而MSE在这种情况下的表现就很好，即便使用固定的学习率也可以有效收敛。MSE损失的梯度随损失增大而增大，而损失趋于0时则会减小。这使得在训练结束时，使用MSE模型的结果会更精确。

所以，如何选择MAE、MSE、RMSE：

• 若异常点代表在商业中很重要的异常情况，并且需要被检测出来，则选用MSE；
• 若只把异常值当作受损数据，则选用MAE
  处理异常点时，MAE损失函数更稳定，但它的导数不连续，因此求解效率较低。MSE损失函数对异常点更敏感，但通过令其导数为0，可以得到更稳定的封闭解。

交叉熵损失与均值平方差损失是机器学习中常用的求损失函数的方式，其中交叉熵损失（Cross Entropy）一般针对的是分类问题，而均值平方差损失（MSE）主要针对的是回归问题。

交叉熵损失是KL散度的简化，在了解交叉熵之前，需要对信息论中熵的含义有基本的了解。

4.1.1信息熵

熵：是关于不确定性的描述，指的是整个系统内部样本之间的距离，或称之为系统内样本分布的集中程度、分散程度和混乱程度。
系统内样本越分散，信息熵就越大；分布越有序，信息熵就越小。
信息的大小和随机事件的概率有关，概率越小的事件发生，信息量就越大；概率越大的事件发生，信息量就越小，所以信息的度量应依赖于概率分布p(x)。

假设一离散型数据X=（x0,x1,x2）,对应的概率为p(xi)。其中每个事件的信息量为： I(xi)=−log(p(xi))，根据熵的定义可得：

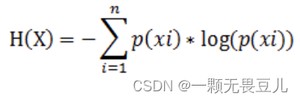
分析上式：

• 对概率取负对数表示了一种可能事件发生时候携带出的信息量
• 把各种可能表示出的信息量乘以其发生的概率之后求和，就表示了整个系统所有信息量的一种期望值。
  综上，熵是表示信息量的期望，即平均信息量，而信息量与概率成反比，即概率越大的事件发生时所获得的信息量就越小，概率越小的事件发生时所获得的信息量就越大。

4.1.2KL散度

KL散度用于衡量两个概率分布之间的差异，值越小，表示两个分布就越接近。
公式如下：
离散形式：

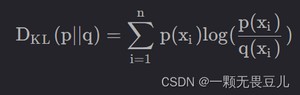
连续形式：

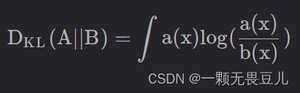
特点：

• 非对称性。KL(p||q)≠KL(q||p)，KL散度用来度量两个分布的相似度或者距离，但KL散度本身并不是距离。
• 非负性。当p(x)和q(x)两个分布完全相同时，其值为0
• 不满足三角不等式
  本质上，KL散度度量的是两者间的信息损失，而不是两者之间的距离。

4.1.3JS散度

JS散度用于衡量两个概率分布的差异度，是KL散度的变体。
公式如下：

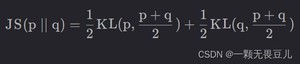
• 解决了KL散度非对称的问题，即满足：JS(p||q)=JS(q||p)
• 取值范围:[0,1]

4.1.4交叉熵

交叉熵常作为多分类问题的损失函数，用来作为预测值和真实值的距离度量。
给定两个概率分布p，q，p(x)表示正确分布，即真实值的分布，q(x)表示预测分布，即预测值的分布。

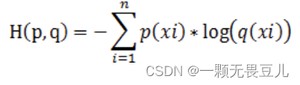
• 描述了两个概率分布间的距离
• 交叉熵越小，两个概率分布越接近

4.1.5KL散度、信息熵、交叉熵三者的关系

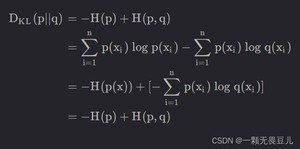
KL散度=信息熵+交叉熵
交叉熵损失常用于分类问题，而且离散的变量，具体是为啥呢？
因为目标是训练模型使得模型拟合的分布与数据的真实分布差异尽可能小，便想到KL散度
数据集的真实值是确定的，即信息熵H§是确定的常数，因此最小化交叉熵即可。

均方误差（Mean Square Error）简称MSE，公式如下：

其中y_i表示真实值，比如模型的真实，比如模型的label；“y_i尖”是预测值，如常用的y_pred。
MSE的范围：[0,+∞)，预测值和真实值完全吻合时，MSE=0，即完美模型（实际模型训练中，基本不会出现的啦！！！）；误差越大，MSE该值越大。

• 交叉熵损失常用于分类问题，而且离散的变量
• 均方误差损失常用于回归问题，而且是连续的变量

鲁棒性：指的是模型对于输入数据的健壮性，即模型在遇到各种不同的数据输入时，仍然能够保持高效的表现。一个鲁棒性强的模型能够在噪声、缺失数据或者其他异常情况下也能够准确地预测结果。

泛化性：则是指模型对于新数据的适应能力，即模型能否对于未在训练集中出现的数据进行准确的预测。一个具有很强泛化性的模型能够在不同的数据集上都表现出色，而不仅仅是在训练集上表现好。

通俗点说，鲁棒性关注的是模型对于已知情况的适应能力，而泛化性则关注的是模型对于未知情况的适应能力。深度学习中的目标是构建既有鲁棒性又有泛化性的模型，即能够在多种情况下都能够高效准确预测结果的模型。
https://blog.csdn.net/weixin_/article/details/

（常总结，常复盘，如有问题，欢迎指出、欢迎讨论！！！）

版权声明：

本文来源网络，所有图片文章版权属于原作者，如有侵权，联系删除。

本文网址：https://www.mushiming.com/mjsbk/7882.html